Рейтинг: 4.1/5.0 (1857 проголосовавших)Категория: Windows: Математика
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
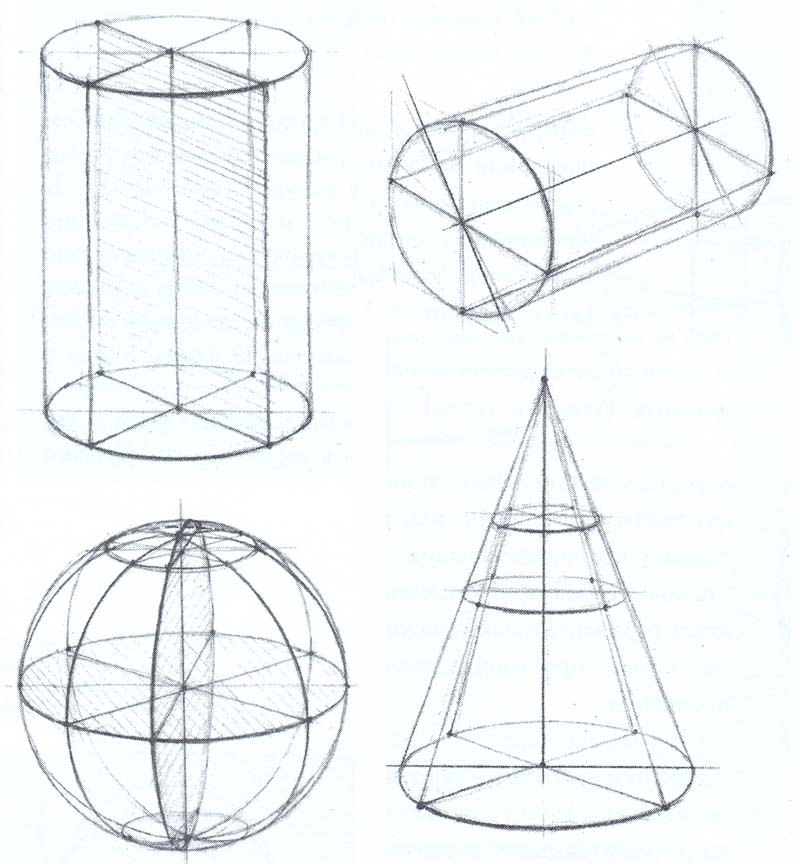
Подписи к слайдам:Презентация на тему: «Тела вращения» Составители: ученицы 11 «а» классаЮщенко ЕкатеринаГузовская ВикторияРуководитель: Войшвилова Марина Николаевна Содержание. Введение………………………………………. 3Цилиндр………………………………………… 7Конус……………………………………………. 17Шар………………………………………………. 29Список использованной литературы……………………………………. 36 Понятие о поверхностях и телах вращения. Представим себе, что плоский многоугольник АВСDE вращается вокруг прямой АВ. При этом каждая его точка не принадлежащая прямой АВ, описывает окружность с центром на этой прямой. Весь многоугольник, вращаясь вокруг прямой, описывает некоторое тело вращения. Плоскость симметрии и осевое сечение Плоскость, проходящая через ось тела вращения, является его плоскостью симметрии. Таких плоскостей каждое тело вращения имеет бесконечно много. Любая плоскость, проходящая через ось тела вращения, пересекает это тело. Полученное сечение называют осевым. Они все равны. Как задать тело вращения: Чтобы задать тело вращения, достаточно указать его ось и фигуру, вращением которой получено данное тело. Например: «тело, образованное вращением треугольника вокруг его стороны.» Виды цилиндров: Определение цилиндра: Цилиндр – это тело, которое состоит из двух кругов, совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих кругов.
Составляющие цилиндра: Развертка цилиндра Сечения цилиндра:
Показать еще
Презентация на тему: " Тела вращения Объёмы тел вращения. Тела вращения Телом вращения называется такое тело, которое плоскостями, перпендикулярными некоторой прямой (оси вращения)," — Транскрипт:1 Тела вращения Объёмы тел вращения 
2 Тела вращения Телом вращения называется такое тело, которое плоскостями, перпендикулярными некоторой прямой (оси вращения), пересекается по кругам с центрами на этой прямой. Телом вращения называется такое тело, которое плоскостями, перпендикулярными некоторой прямой (оси вращения), пересекается по кругам с центрами на этой прямой. Ось вращения 
3 Объём цилиндра Объём цилиндра равен произведению площади основания на высоту. Объём цилиндра равен произведению площади основания на высоту. 
4 Объём конуса Объём конуса равен одной трети произведения площади основания на высоту. Объём конуса равен одной трети произведения площади основания на высоту. 
5 Объём усечённого конуса 
6 Вывод формулы для объёмов тел вращения X Y 0 Y=f(x) 
7 Вывод формулы для объёмов тел вращения X Y 0 Y=f(x) X V(x) 
8 Вывод формулы для объёмов тел вращения X Y 0 Y=f(x) X h X+h V(x+h) - V(x)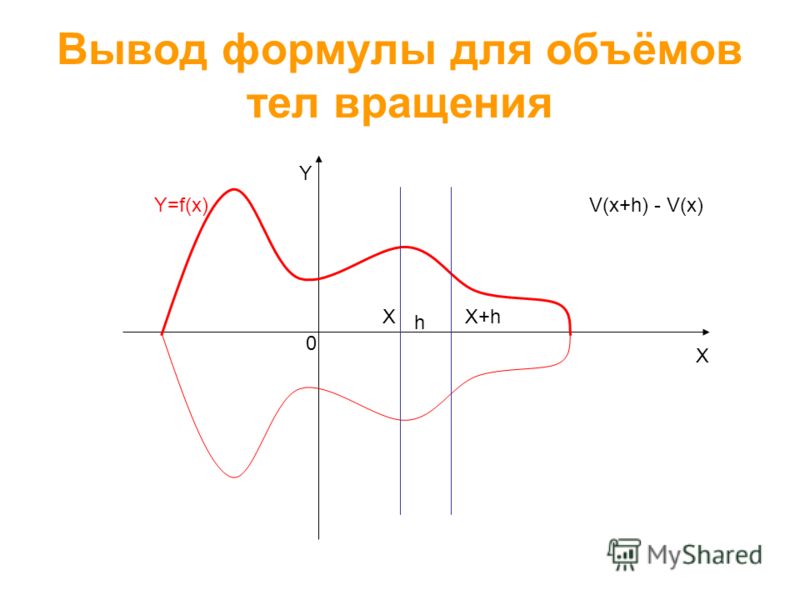 
9 Вывод формулы для объёмов тел вращения X Y 0 Y=f(x) X h X+h V(x) V(x+h) - V(x) M m М m h 
10 Вывод формулы для объёмов тел вращения 
12 Шар: история Оба слова "шар" и "сфера" происходят от одного и того же греческого слова "сфайра" - мяч. При этом слово "шар" образовалось от перехода согласных сф в ш. В древности сфера была в большом почёте. Астрономические наблюдения над небесным сводом неизменно вызывали образ сферы. Оба слова "шар" и "сфера" происходят от одного и того же греческого слова "сфайра" - мяч. При этом слово "шар" образовалось от перехода согласных сф в ш. В древности сфера была в большом почёте. Астрономические наблюдения над небесным сводом неизменно вызывали образ сферы. 
13 Шары из жизни 
14 Гигантский шар в игрушечном городе Это - космический корабль "Земля", рсположенный на окраине ДИСНЕЙЛЕНДА в штате Флорида. По задумке эта сферическая конструкция должна оли- цетворять будущее человечества. Это - космический корабль "Земля", рсположенный на окраине ДИСНЕЙЛЕНДА в штате Флорида. По задумке эта сферическая конструкция должна оли- цетворять будущее человечества. 
15 Вывод формулы объёма шара Y X 0 - RR 
16 Вывод формулы объёма шара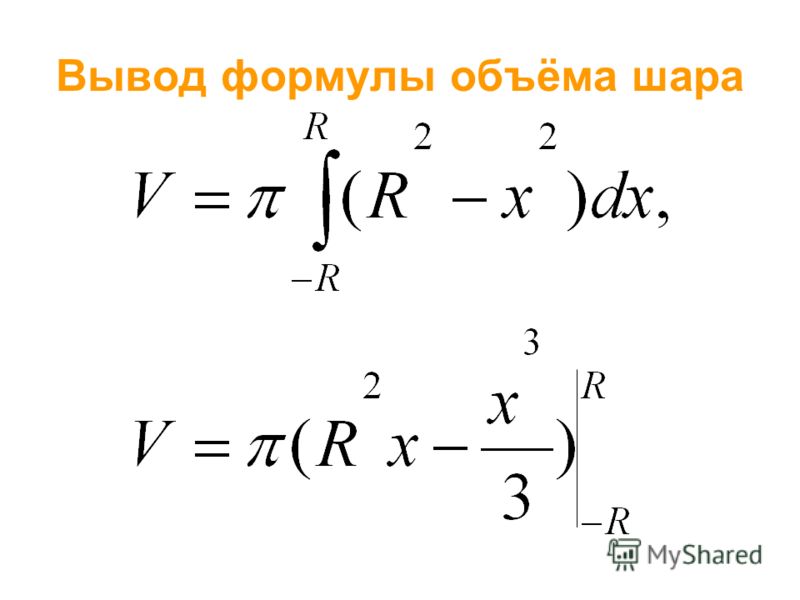 
17 Объём шара Объём шара равен Объём шара равен 
18 Шаровой сегмент Шаровым сегментом называется часть шара, отсекаемая от него плоскостью. Шаровым сегментом называется часть шара, отсекаемая от него плоскостью. 
19 Объём шарового сегмента Объём шарового сегмента равен Объём шарового сегмента равен Здесь R – радиус шара, а H – высота шарового сегмента. Здесь R – радиус шара, а H – высота шарового сегмента. 
20 Шаровой сектор Шаровым сектором называется тело, которое получается из шарового сегмента и конуса следующим образом. Шаровым сектором называется тело, которое получается из шарового сегмента и конуса следующим образом. Если шаровой сегмент меньше полушара, то шаровой сегмент дополняется конусом, у которого вершина в центре шара, а основанием является основание сегмента. Если шаровой сегмент меньше полушара, то шаровой сегмент дополняется конусом, у которого вершина в центре шара, а основанием является основание сегмента. Если сегмент больше полушара, то указанный конус из него удаляется. Если сегмент больше полушара, то указанный конус из него удаляется. 
21 Объём шарового сектора Объём шарового сектора равен Объём шарового сектора равен Здесь R – радиус шара, а H – высота соответсвующего шарового сегмента. Здесь R – радиус шара, а H – высота соответсвующего шарового сегмента. 
За площадь боковой поверхности цилиндра принимается площадь его развертки: Sбок = 2?rh.
За площадь боковой поверхности конуса принимается площадь ее развертки: Sбок = ?rl Площадь полной поверхности конуса: Sкон = ?r(l+ r)
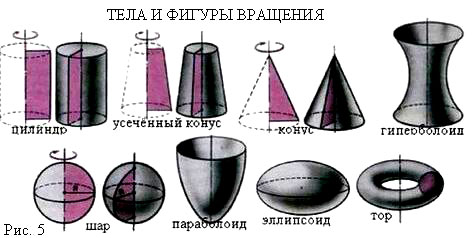
При вращении контуров фигур возникает поверхность вращения (например, сфера. образованная окружностью ), в то время как при вращении заполненных контуров возникают тела (как шар, образованный кругом ).
Объём и площадь поверхности тел вращения Примечания Смотреть что такое "Тела вращения" в других словарях:деталь с закрытым уступом – тела вращения — Часть детали, поверхность которой ограничена с обеих сторон поверхностями вращения, имеющими больший диаметр. Наличие закрытых уступов не влияет на определение ступенчатости наружной поверхности. Проточки для выхода инструмента не считается… … Справочник технического переводчика
Тонкого тела теория — теория пространственного безвихревого течения идеальной жидкости около тонких тел (тела, у которых поперечный размер l (толщина, размах) мал по сравнению с продольным размером L: (?) = l/L >
Рассмотрим тело, образованное вращением вокруг оси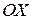 
фигуры, ограниченной непрерывной кривой 
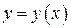, осью 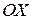и прямыми 
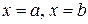(рис. 7). Разобьем отрезок 
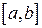на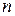 
частей точками 
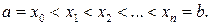Проведем через точки деления плоскости, перпендикулярные оси 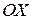. Сечение тела вращения плоскостью 
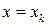есть круг радиусом 
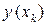с площадью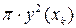 
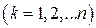. Проведенные плоскости разобьют тело на слои. Каждый 
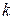-й слой
приближенно заменим прямым цилиндром (рис. 7) с радиусом 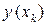, высотой 
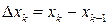и объемом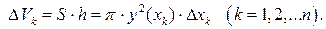 
Сумма объемов всех цилиндров равна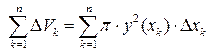 
.
Объем тела вращения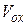 
определяется как предел этой суммы
при стремлении к нулю величины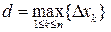 
. Мы получили предел интегральной суммы непрерывной функции 
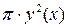по отрезку 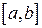, который существует и равен интегралу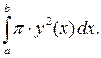 
Итак, объем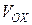 
тела, полученного при вращении вокруг оси 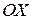фигуры, ограниченной кривой 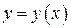, осью 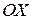и прямыми 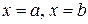, вычисляется по формуле
Аналогично вычисляется объем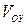 
тела, полученного при вращении вокруг оси 
фигуры, ограниченной линией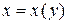 
, осью , прямыми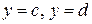 
(рис. 8):
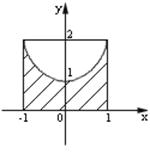Пример 1. Вычислить объем тела, образованного вращением фигуры, ограниченной линиями 
,
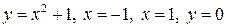а) вокруг оси 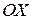, б) вокруг оси .
Решение. Построим параболу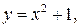 
прямые 
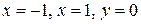и заштрихуем фигуру, ограниченную этими линями (рис. 31).
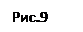а). Объем тела, полученного при вращении этой фигуры вокруг оси 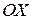, вычислим по формуле:
Подынтегральная функция − четная, поэтому используем следствие 2 к теореме.
б). Для вычисления объема тела вращения фигуры вокруг оси нельзя непосредственно воспользоваться формулой, так как фигура сверху ограничена не прямой, а параболой. Поэтому сначала рассмотрим фигуру, ограниченную прямой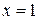 
, осью , прямыми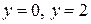 
. При ее вращении вокруг оси получим цилиндр, объем которого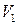 
можно вычислить по формуле 
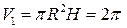или по формуле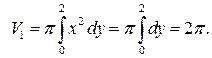 
Теперь рассмотрим фигуру, ограниченную линиями 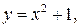осью и прямой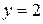 
. При ее вращении вокруг оси получим тело, объем которого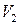 
вычислим по формуле: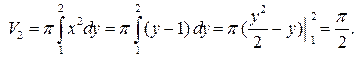 
Тогда искомый объем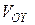 
будет равен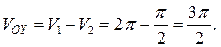 
7. Лекционное занятие. КРИВОЛИНЕЙНЫЙ ИНТЕГРАЛ ПЕРВОГО РОДА
Случай 1. Пусть на плоскости дуга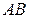 
задана уравнением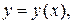 
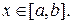Будем предполагать, что функция 
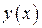непрерывна вместе со своей производной на .
Рассмотрим на кривой точки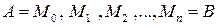 
с абсциссами 
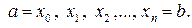Проведем хорды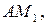 
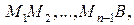длины которых обозначим 
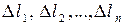(рис. 1).
Вычислим длину 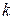-й хорды
Для вычисления приращения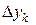 
воспользуемся формулой конечных приращений Лагранжа
где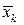 
− некоторая точка из промежутка 
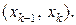Тогда длина 
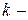й хорды
Учтем это и возьмем в определении криволинейного интеграла в качестве промежуточных точек на дугах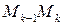 
точки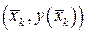 
:
Мы получили предел интегральной суммы функции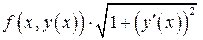 
по отрезку 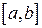, который равен интегралу 
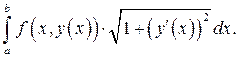Следовательно,
Итак, для вычисления криволинейного интеграла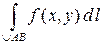 
по дуге АВ с уравнением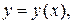 
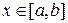нужно:
1) заменить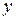 
в подынтегральной функции на его значение 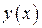на дуге;
2) заменить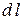 
на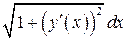 
;
3) вычислить получившийся определенный интеграл по отрезку .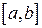
Иногда удобнее использовать уравнение кривой в виде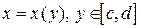 
. Тогда
Пример 1. Вычислить длину дуги кривой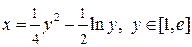 
.
Решение. Уравнение кривой разрешено относительно 
, поэтому воспользуемся формулой (7.16), учитывая, что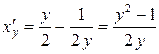 
,
Случай 2. Пусть на плоскости дуга 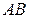задана параметрическими уравнениями
причем функции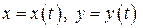 
непрерывны на 
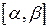вместе со своими производными и 
.
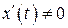Для определенности, пусть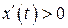 
. Уравнения 
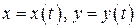определяют функцию 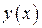, которая имеет непрерывную производную 
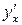. Учитывая, что 
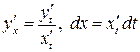, получим 
.
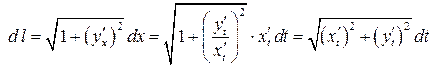Итак, справедливы следующие формулы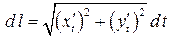 
и
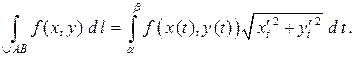Аналогично, для пространственной кривой, заданной параметрическими уравнениями 
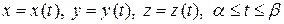, имеем
Пример 2. Найти массу верхней полуокружности радиуса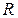 
, если плотность 
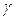в каждой ее точке равна ординате этой точки.
Решение. Масса кривой вычисляется с помощью криволинейного интеграла:
Для вычисления интеграла запишем параметрические уравнения окружности: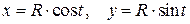 
.
Понятие тела и поверхности вращения. Цилиндр. Осевое сечение цилиндра. Сечение цилиндра плоскостью. Вписанные и описанные призмы и цилиндры
Тело вращения называется тело, пересекается по кругам с центрами на некоторой прямой плоскостями, перпендикулярными к этой прямой. Простейшими телами вращения является цилиндр, конус, шар.
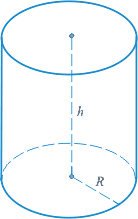
Цилиндр — это тело, которое состоит из двух кругов, лежащих в разных плоскостях и совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки данных кругов.
Основами цилиндра имеются круги, образующими цилиндра являются отрезки, соединяющие соответствующие точки окружностей данных кругов.
Радиусом цилиндра является радиус его основания. Высотой цилиндра является расстояние между основаниями.
Свойства цилиндра:
— Основания цилиндра уровне;
— Основания цилиндра лежат в параллельных плоскостях;
— Образующие цилиндра параллельны и равны;
— Сечение цилиндра плоскостью, параллельной его оси, представляет собой прямоугольник.
Сечение цилиндра плоскостью, параллельной его основе, круг, равна окружности основания.
Цилиндр называется прямым, если его образующие перпендикулярны плоскостям основания.
Осью цилиндра называется прямая, проходящая через центры оснований. Ось цилиндра параллельна его образующим.
Поверхность цилиндра состоит из оснований и боковой поверхности.
Сечение цилиндра плоскостью, параллельной его оси, представляет собой прямоугольник, две стороны которого образующие цилиндра, а две другие — параллельные хорды его основ.
Осевым сечением цилиндра называется сечение, проходящей через его ось. Осевое сечение цилиндра является прямоугольником.
Цилиндр, осевой сечение которого является квадратом. называется равносторонним цилиндром.
Призмой, вписанной в цилиндр. называется такая призма, у которой плоскостями оснований являются плоскости оснований цилиндра, а боковыми ребрами — образующие цилиндра.
Касательной плоскостью к цилиндру называется плоскость, проходящая через образующую цилиндра и перпендикулярная плоскости осевого сечения, содержащей эту плоскость.
Призмой, описанной вокруг цилиндра. называется призма, у которой плоскостями оснований являются плоскости оснований цилиндра, а плоскости боковых граней являются касательными плоскостями к цилиндру.
Неопределенный интеграл. Объем тела вращения. Эмпирическая формула. Сходимость ряда. Вычисление объема тела, образованного вращением вокруг оси ОХ фигуры, ограниченной линиями. Исследование на условную сходимость по признаку Лейбница.
контрольная работа [25,8 K], добавлен 27.05.2004
Возникновение геометрии как науки о формах, размерах и границах частей пространства, которые в нем занимают вещественные тела. Появление геометрии в Греции к концу VII в. до н. э. Теорема Пифагора и развитие методов аналитической геометрии Гаусса.
реферат [38,5 K], добавлен 16.01.2010
Нахождение статических моментов и центра тяжести кривой. Нахождение статических моментов и центра тяжести плоской фигуры. Первая и вторая теоремы Гульдина. Нахождение объема тела вращения плоской фигуры. Использование интеграла вместо обыкновенной суммы.
курсовая работа [275,3 K], добавлен 30.12.2011
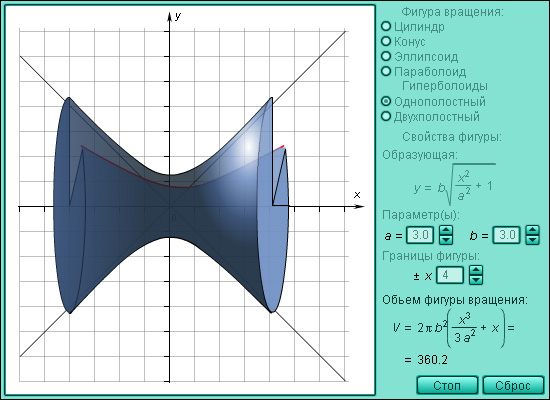
Фигуры вращения правильных многогранников, использование их теории. Виды поверхностей в фигурах вращения. Теорема о пересечении гиперболической и цилиндрической поверхностей вращения. Классификация задач на вращение многогранников и вычисление объемов.
реферат [1,1 M], добавлен 25.09.2009
Поиск площади фигуры, ограниченной графиками функций с помощью двойного интеграла. Получение вращением объема тела вокруг оси ОХ фигуры, ограниченной указанными линиями. Пределы интегрирования в двойном интеграле по области, ограниченной линиями.
контрольная работа [166,9 K], добавлен 28.03.2014
Криволинейный интеграл первого рода. Двойной интеграл в декартовой и полярной системе координат. Интеграл по поверхности (первого рода). Приложение определенного интеграла в геометрии: площадь плоской фигуры и цилиндрической поверхности, объем тела.
методичка [517,1 K], добавлен 27.01.2012
Страницы биографии древнегреческого философа и математика Пифагора. Теорема Пифагора: основные формулировки и методы доказательства. Обратная теорема Пифагора. Примеры задач на применение теоремы Пифагора. "Пифагоровы штаны" и "тройка", "дерево Пифагора".
научная работа [858,3 K], добавлен 29.03.2011
Производные функций, заданных в явном и неявном виде. Исследование функций методами дифференциального исчисления. Точки перегиба и экстремума, градиент функции. Объем тела, образованного вращением фигуры и ограниченной графиками функций, вокруг оси.
контрольная работа [77,3 K], добавлен 11.07.2013
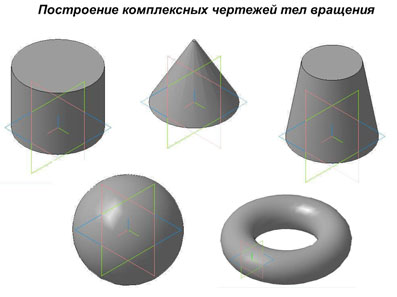
Определение цилиндра (кругового прямого и наклонного), прямого и усечённого конуса, шара и сферы. Основные формулы по расчету геометрических размеров фигур вращения: радиуса, площади боковой и полной поверхности. Объем шара по Архимеду. Уравнение сферы.
презентация [3,4 M], добавлен 18.04.2013
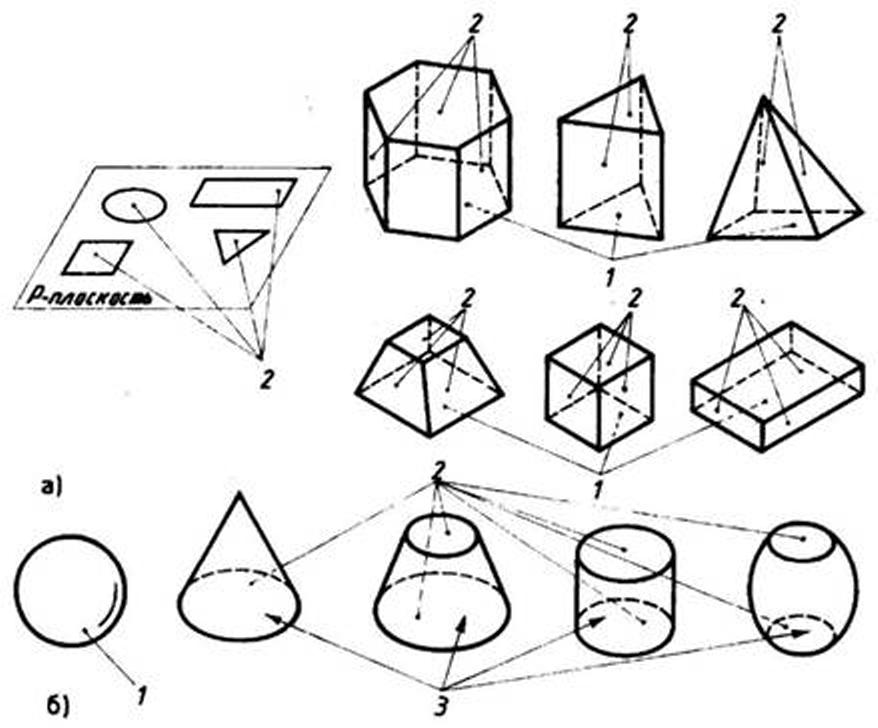
Замкнутые пространственные фигуры, ограниченные плоскими многоугольниками. Линейчатые поверхности вращения. Точка на поверхности тора и сферы. Понятие меридиональной плоскости. Преобразование комплексного чертежа. Метод замены плоскостей проекций.
презентация [69,8 K], добавлен 27.10.2013
Размещено на http://www.allbest.ru/
по теме: "Фигуры и тела вращения"
Михайлова Дмитрия Петровича
Учитель математики:
Шумилова А.Н.
1. “Предмет математики настолько серьёзен, что надо не упускать возможности сделать его немного занимательным”. - Б. Паскаль
· научить применять знания при решении нестандартных задач, видеть в них простые составляющие;
· показать целостность и гармонию окружающего мира, взаимосвязь изучаемых предметов, взаимосвязь разделов математики, красоту математики;
· воспитывать чувство хозяина своей судьбы, воспитывать любовь к прекрасному.
Оборудование. Модель к основной задаче - сфера с сечениями, выполненная из пяльцев для вышивания. Модели: цилиндр, конус, усечённый конус, шар. Бублик, яйцо, горн или труба, юла, луковица, свеча, глобус. Пластинки для сборки гиперболоида вращения. Портреты С. Ковалевской, Н. Лобачевского. Плакаты: “Тела и фигуры вращения”, об атласе Г. Меркатора, с высказыванием М. Монтеня, “Математика и история”. Рисунки башни радиостанции В.Г. Шухова, “седла”, псевдосферы Лобачевского, купола, юлы.
2. Кроссворды “Тела и фигуры вращения”, тексты с условием задачи
План - конспект занятия.
1. Игровой момент перед занятием: разгадывание двух кроссвордов “Тела и фигуры вращения” по группам. Можно завершить в конце занятия,используя новые знания.
2. Эмоциональный настрой. Великий Омар Хайям - математик, поэт, философ. Он призывает быть хозяевами своей судьбы. Слушаем отрывок из его произведения:
Ты скажешь, эта жизнь - одно мгновенье. Её цени, в ней черпай вдохновенье. Как проведёшь её, так и пройдёт. Не забывай: она - твоё творенье.
3. Постановка задач, ознакомление с планом данного занятия.
4. Обзор учащегося “Математика и история”(полная информация - на плакате).
5. Сообщение о проекции Г.Меркатора, о его атласе. Поверхность шара и карта мира
6. Знания о сфере пришли из астрономии. Омар Хайям писал:
От земной глубины до далёких планет Мирозданья загадкам нашёл я ответ. От зенита Сатурна до чрева Земли Тайны мира своё толкованье нашли.
7. Показать рисунок и модель “Седла” (пример криволинейной поверхности), рисунок Псевдосферы Лобачевского.
8. Работа с плакатом “Тела и фигуры вращения”, с моделями (цилиндр, конус, усечённый конус, шар).
9. Решение основной задачи.
10. Продолжаем работу с плакатом. Изучаем параболоид, эллипсоид, гиперболоид. Отвечаем на вопрос, при вращении какой кривой получается каждая из фигур.
11. Сообщение о башне радиостанции в Москве на Шаболовке.
12. Вопросы в стихотворной форме о торе и юле.
13. Красота и математика, гармония и духовность. Геометрия купола храма.
14. Проверка кроссвордов.
15. Области применение знаний о телах и фигурах вращения.
16. Сборка гиперболоида вращения. Пластмассовые пластинки детского конструктора.
17. Задание на дом: сочинить вопросы о телах вращения, стихи или кроссворды.
18. Подведение итогов.
“Тела и фигуры вращения”
Вопросы к кроссворду - 1
По горизонтали. 1. Фигура на плоскости, все точки которой расположены не далее данного расстояния от одной точки. 2. Прямая, при вращении которой вокруг оси образуется боковая поверхность цилиндра, конуса. 3. Тело, полученное вращением прямоугольника вокруг одной из его сторон. 4. Угол между высотой и плоскостью основания конуса. 5. Тело, полученное вращением круга вокруг оси, лежащей в плоскости круга и не пересекающей его.
По вертикали. 1. Тело, полученное вращением прямоугольного треугольника вокруг одного из его катетов. 2. Плоская фигура, при вращении которой образуется усечённый конус. 3.Тело вращения, являющееся верхней частью архитектурного сооружения. 4. Отрезок, соединяющий две точки сферы и проходящий через центр шара. 5. Тело, полученное вращением полукруга вокруг его диаметра. 6. Фигура, полученная вращением полуокружности вокруг её диаметра. 7. Тело вращения, об устойчивости движения которого написана известная работа великой русской женщины - математика.
Вопросы к кроссворду - 2
По горизонтали. 1. Фигура, полученная вращением параболы вокруг её оси. 2. Отрезок, соединяющий центр сферы с любой её точкой. 3. Круг, являющийся элементом конуса, плоскость которого перпендикулярна оси конуса. 4. Музыкальный инструмент, часть которого напоминает Псевдосферу Лобачевского. 5. Отрезок, соединяющий две точки окружности.
По вертикали. 1. Фигура, полученная вращением гиперболы вокруг её оси. 2. Перпендикуляр, опущенный из вершины конуса на плоскость основания. 3. Тело, полученное вращением круга вокруг оси, лежащей в плоскости круга и не пересекающей его. 4. Тело, полученное вращением полукруга вокруг его диаметра. 5. Фигура, полученная вращением полуокружности вокруг её диаметра. 6. Тело вращения, принцип движения которого описала великая русская женщина-математик. 7. Фигура, полученная вращением эллипса вокруг её оси.
Ответы к кроссворду - 1.
По горизонтали. 1. Круг. 2.Образующая. 3. Цилиндр. 4. Прямой. 5. тор.
По вертикали. 1. Конус. 2. Трапеция.3. Купол. 4. Диаметр. 5. Шар. 6. Сфера. 7. Юла.
Ответы к кроссворду - 2.
По горизонтали. 1. Параболоид. 2.Радиус. 3. Основание. 4. Труба. 5. Хорда.
По вертикали. 1. Гиперболоид. 2.Высота. 3. Тор. 4. Шар. 5. Сфера. 6. Юла. 7. Эллипсоид.
Телом вращения называется тело, образованное в результате вращения какой - либо линии вокруг прямой.
Цилиндром (круговым цилиндром) называется тело, которое состоит из двух кругов, не лежащих в одной плоскости и совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих кругов. Круги называется основаниями цилиндра, а отрезки, соединяющие соответствуете точки окружностей кругов, - образующими цилиндра.
Так как параллельный перенос есть движение, то основания цилиндра равны. Так как при параллельном переносе плоскость переходит в параллельную плоскость, то у цилиндра основания лежат в параллельных плоскостях. Так как при параллельном переносе точки смещаются по параллельным прямым на одно и то же расстояние, то у цилиндра образующие параллельны и равны. Поверхность цилиндра состоит из оснований и боковой поверхности.
Радиусом цилиндра называется радиус его основания. Высотой цилиндра называется расстояние между плоскостями его оснований. Осью цилиндра называется прямая, проходящая через центры оснований.
Цилиндр называется прямым, если его образующие перпендикулярны плоскостям оснований. Мы будем рассматривать только прямой круговой цилиндр, называя его для краткости просто цилиндром.
Цилиндр может быть получен вращением прямоугольника вокруг одной из его сторон. На рисунке изображен цилиндр, полученный вращением прямоугольника ABCD вокруг стороны АВ. При этом боковая поверхность цилиндра образуется вращением стороны CD, а основания - вращением сторон ВС и AD.
Сечения цилиндра1) Если секущая плоскость проходит через ось цилиндра, то сечение представляет собой прямоугольник (см. рис.), две стороны которого — образующие, а две другие - диаметры оснований цилиндра. Такое сечение называется осевым.
На этом уроке мы познакомимся с новым способом создания объектов – с так называемыми телами вращения, начнем знакомство со стеком модификаторов объектов и новым видом объектов – сплайнами.
Итак, что такое тела вращения? Если верить википедии, то Тела вращения — объёмные тела, возникающие при вращении плоской фигуры, ограниченной кривой, вокруг оси, лежащей в той же плоскости. Т.е. как пример можно привести такие объекты как шар, конус, цилиндр и т.д. Все эти фигуры уже есть среди стандартных объектов, но к телам вращения так же относятся более сложные объекты такие как тарелки, бутылки, кружки, стаканы, рюмки и др. Вот как раз некоторые из этих объектов мы сегодня и сделаем. Начнем пожалуй с более легкой для моделирования бутылки.
Запускаем 3d Max, если он уже запущен то создаем новую сцену. Во вкладке «Create»
Выбираем пункт «Shapes»
В выпадающем списке выбираем «Splines»(Сплайны)
В рабочей области надо перейти в один из видов проекции, например в вид слева, там гораздо удобнее работать со сплайнами. Собственно что такое сплайн? У этого понятия есть довольно сложное для простого человека определение, но по простому это некоторая линия которая проходит через контрольные точки и плавно (или не совсем плавно) их огибает.
Продолжим. Выбираем объект «Line»
И пробуем изобразить бутылку в разрезе, причем не всю бутылку а только ее половину. Врятли это у вас это получится с первого раза, особенно без чертежа (про использование чертежей для моделирования поговорим в следующих уроках), поэтому набросайте примерный контур бутылки, который потом можно редактировать.
При создании можно регулировать плавность линии, так если нажать левую кнопку мыши (поставить контрольную точку) и тут же ее отпустить то получится ломаная линия:
Если поставить точку (нажав левую кнопку мыши), и не отпустить кнопку мыши то таская курсор по экрану можно регулировать плавность линии на участке от предыдущей точки до новой точки (на рисунке показан красной стрелкой):
После отпускания левой кнопки мыши регулируется плавность лини на участке от созданной точки до следующей точки (на рисунке показан красной стрелкой):
Для простоты при создании контура я использовал только ломаные линии. У меня получилось примерно так:
Обратите внимание что, это один сплайн, а не несколько различных сплайнов расположенных один за другим. Так же важным фактом является то, что сплайн имеет разрыв и это разрыв внизу, на дне бутылки.
Теперь придадим плавности нашему контуру, для этого выделим созданный контур (если выделение было снято) и перейдем на вкладку «Modify»
Здесь обратите внимание на вот такой список:
Выбирая отдельные пункты этого списка можно редактировать соответствующие части сплайна. Выбрав корень этого списка, т.е. надпись «Line» мы получим доступ целиком ко всему объекту, Выбрав «Vertex», можно будете редактировать вершины (контрольные точки) сплайна, т.е двигать их, менять их тип и т.д. «Segment» – отвечает за работу с сегментами сплайна (участками между вершинами) “Spline” – позволяет изменять целиком часть сплайна, не связанную с другой частью.
Эти же вкладки продублированы ниже в свитке «Selection»:
Нам нужно править вершины сплайна поэтому выделяем вкладку «Vertex», теперь с помощью инструмента «Select and Move»
можно перетащить каждую вершину в нужное место. Если нажать правую кнопку мышки на одной из вершин откроется контекстное меню где можно изменить тип вершины:
Доступны следующие типы:
Bezier Corner – вершина имеет независимые друг от друга плечи силы (желтые палочки), регулируя которые можно изменять участки сплайна до и после вершины:
Bezier – так же как и предыдущий тип имеет два плеча но зависимых друг от друга, так двигая одно плечо двигается и другое, так что вместе они образуют прямую:
Corner – простая ломаная вершина без плавного обвода:
Smooth – не регулируемый плавный обвод вершины:
Теперь двигая вершины, меняя их тип и настраивая плавность их обводки, попробуйте сделать контур бутылки более правильным и гладким. При этом возможно вам потребуется вставить лишнею вершину, там где требуется дополнительная детализация, для этого есть кнопка “Insert” в свитке “Geometry”:
Нажав на нее можно вставить вершину в нужном месте сплайна щелкнув левой клавишей мыши. Удаление лишних вершин производится нажатием кнопки “Delete” на клавиатуре или тоже кнопки “Delete” в свитке “Geometry”:
При удалении сплайн не разрывается.
Постарайся не увлекаться количеством вершин, чем меньшим количеством вы правильно опишите контуры бутылки, тем лучше. На последок следует упомянуть про то как выделить группу вершин, для этого можно выделять вершины зажав клавишу “Ctrl“ на клавиатуре, или обводя прямоугольной рамкой нужные вершины (зажав левую клавишу мыши). Можно комбинировать эти два способа, зажав “Ctrl“ обводить нужные вершины.
