Золотое сечение

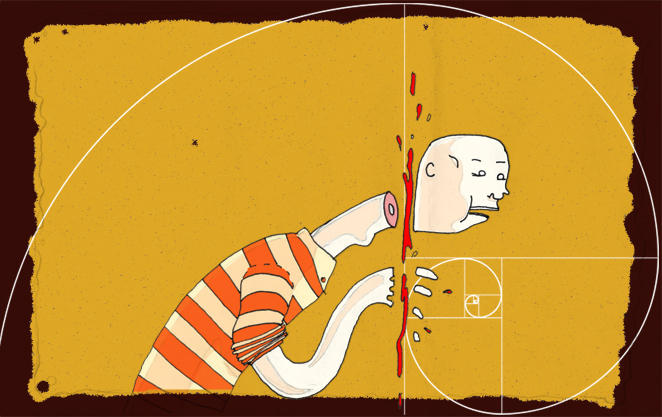
ИЛЛЮЗИЙ И ИНТЕЛЛЕКТУАЛЬНЫХ РАЗВЛЕЧЕНИЙ Стоит ли доверять всему, что вы видите? Можно ли увидеть то, что никто не видел? Правда ли, что неподвижные предметы могут двигаться? Почему взрослые и дети видят один и тот же предмет по разному? На этом сайте вы найдете ответы на эти и многие другие вопросы. Log-in.ru© - мир необычных и интеллектуальных развлечений. Интересные оптические иллюзии, обманы зрения, логические флеш-игры. Золотое сечение

Золотое сечение – это такое пропорциональное деление отрезка на неравные части, при котором меньший отрезок так относится к большему, как больший ко всему.

a. b = b. c или с. b = b. а.

Эта пропорция равна: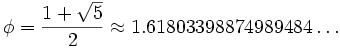

К примеру, в правильной пятиконечной звезде, каждый сегмент делится пересекающим его сегментом в золотом сечении (т. е. отношение синего отрезка к зелёному, красного к синему, зелёного к к фиолетовому, равны 1.618

Принято считать, что понятие о золотом сечении ввел в научный обиход Пифагор. Есть предположение, что Пифагор свое знание позаимствовал у египтян и вавилонян. И действительно, пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании.

В 1855 г. немецкий исследователь золотого сечения профессор Цейзинг опубликовал свой труд «Эстетические исследования».

Цейзинг измерил около двух тысяч человеческих тел и пришел к выводу, что золотое сечение выражает средний статистический закон.

Золотые пропорции в частях тела человека

Деление тела точкой пупа – важнейший показатель золотого сечения. Пропорции мужского тела колеблются в пределах среднего отношения 13. 8 = 1,625 и несколько ближе подходят к золотому сечению, чем пропорции женского тела, в отношении которого среднее значение пропорции выражается в соотношении 8. 5 = 1,6.

У новорожденного пропорция составляет отношение 1. 1, к 13 годам она равна 1,6, а к 21 году равняется мужской.

Пропорции золотого сечения проявляются и в отношении других частей тела – длина плеча, предплечья и кисти, кисти и пальцев и т.д.

Справедливость своей теории Цейзинг проверял на греческих статуях. Наиболее подробно он разработал пропорции Аполлона Бельведерского. Подверглись исследованию греческие вазы, архитектурные сооружения различных эпох, растения, животные, птичьи яйца, музыкальные тона, стихотворные размеры.

Цейзинг дал определение золотому сечению, показал, как оно выражается в отрезках прямой и в цифрах. Когда цифры, выражающие длины отрезков, были получены, Цейзинг увидел, что они составляют ряд Фибоначчи .

Ряд чисел 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 и т.д. известен как ряд Фибоначчи. Особенность последовательности чисел состоит в том, что каждый ее член, начиная с третьего, равен сумме двух предыдущих 2 + 3 = 5; 3 + 5 = 8; 5 + 8 = 13, 8 + 13 = 21; 13 + 21 = 34 и т.д. а отношение смежных чисел ряда приближается к отношению золотого деления.

Так, 21. 34 = 0,617, а 34. 55 = 0,618. (или 1.618. если делить большее число на меньшее).

Ряд Фибоначчи мог бы остаться только математическим казусом, если бы не то обстоятельство, что все исследователи золотого деления в растительном и в животном мире, не говоря уже об искусстве, неизменно приходили к этому ряду как арифметическому выражению закона золотого сечения.

Золотое сечение в искусстве

Еще в 1925 году искусствовед Л.Л.Сабанеев, проанализировав 1770 музыкальных произведений 42 авторов, показал, что подавляющее большинство выдающихся сочинений можно легко разделить на части или по теме, или по интонационному строю, или по ладовому строю, которые находятся между собой в отношении золотого сечения.

Причем, чем талантливее композитор, тем в большем количестве его произведений найдено золотых сечений. У Аренского, Бетховена, Бородина, Гайдна, Моцарта, Скрябина, Шопена и Шуберта золотые сечения найдены в 90% всех произведений. По мнению Сабанеева, золотое сечение приводит к впечатлению особой стройности музыкального сочинения.

В кино С. Эйзенштейн искусственно построил фильм Броненосец Потёмкин по правилам «золотого сечения». Он разбил ленту на пять частей. В первых трёх действие разворачивается на корабле. В двух последних — в Одессе, где разворачивается восстание. Этот переход в город происходит точно в точке золотого сечения. Да и в каждой части есть свой перелом, происходящий по закону золотого сечения.

Золотое сечение в архитектуре, скульптуре, живописи

Одним из красивейших произведений древнегреческой архитектуры является Парфенон (V в. до н. э.).

На рисунках виден целый ряд закономерностей, связанных с золотым сечением. Пропорции здания можно выразить через различные степени числа Ф=0,618.

На плане пола Парфенона также можно заметить "золотые прямоугольники":

Золотое соотношение мы можем увидеть и в здании собора Парижской Богоматери (Нотр-дам де Пари), и в пирамиде Хеопса:

Не только египетские пиpамиды постpоены в соответствии с совеpшенными пpопоpциями золотого сечения; то же самое явление обнаpужено и у мексиканских пиpамид.

Золотая пропорция применялась многими античными скульпторами. Известна золотая пропорция статуи Аполлона Бельведерского: рост изображенного человека делится пупочной линией в золотом сечении.

Переходя к примерам “золотого сечения” в живописи, нельзя не остановить своего внимания на творчестве Леонардо да Винчи. Посмотрим внимательно на картину "Джоконда". Композиция портрета построена на"золотых треугольниках".

Золотое сечение в шрифтах и бытовых предметах

В биологических исследованиях было показано, что, начиная с вирусов и растений и кончая организмом человека, всюду выявляется золотая пропорция, характеризующая соразмерность и гармоничность их строения. Золотое сечение признано универсальным законом живых систем.

Было установлено, что числовой ряд чисел Фибоначчи характеризует структурную организацию многих живых систем. Например, винтовое листорасположение на ветке составляет дробь (число оборотов на стебле/число листьев в цикле, напр. 2/5; 3/8; 5/13), соответствующую рядам Фибоначчи.

Хорошо известна "золотая" пропорция пятилепестковых цветков яблони, груши и многих других растений. Носители генетического кода - молекулы ДНК и РНК - имеют структуру двойной спирали; ее размеры почти полностью соответствуют числам ряда Фибоначчи.

Гете подчеркивал тенденцию природы к спиральности.

Паук плетет паутину спиралеобразно. Спиралью закручивается ураган. Испуганное стадо северных оленей разбегается по спирали.

Гете называл спираль "кривой жизни". Спираль увидели в расположении семян подсолнечника, в шишках сосны, ананасах, кактусах и т.д.

Цветки и семена подсолнуха, ромашки, чешуйки в плодах ананаса, хвойных шишках "упакованы" по логарифмическим ("золотым") спиралям, завивающимся навстречу друг другу, причем числа "правых "и "левых" спиралей всегда относятся друг к другу, как соседние числа Фибоначчи.

Рассмотрим побег цикория. От основного стебля образовался отросток. Тут же расположился первый листок. Отросток делает сильный выброс в пространство, останавливается, выпускает листок, но уже короче первого, снова делает выброс в пространство, но уже меньшей силы, выпускает листок еще меньшего размера и снова выброс.

Если первый выброс принять за 100 единиц, то второй равен 62 единицам, третий – 38, четвертый – 24 и т.д. Длина лепестков тоже подчинена золотой пропорции. В росте, завоевании пространства растение сохраняло определенные пропорции. Импульсы его роста постепенно уменьшались в пропорции золотого сечения.

У многих бабочек соотношение размеров грудной и брюшной части тела отвечает золотой пропорции. Сложив крылья, ночная бабочка образует правильный равносторонний треугольник. Но стоит развести крылья, и вы увидите тот же принцип членения тела на 2,3,5,8. Стрекоза также создана по законам золотой пропорции: отношение длин хвоста и корпуса равно отношению общей длины к длине хвоста.

В ящерице длина ее хвоста так относится к длине остального тела, как 62 к 38. Можно заметить золотые пропорции, если внимательно посмотреть на яйцо птицы.

Кто знает чем интерестно число и почему уже Да винчи нарисовал пирамиду и сказал ето ключ ко всей вселенной (0, 618)

Arkadiy Darchuk Мудрец (11349) 8 лет назад

Итальянский купец Леонардо из Пизы (1180-1240), более известный под прозвищем Фибоначчи был, безусловно, самым значительным математиком средневековья. Роль его книг в развитии математики и распространении в Европе математических знаний трудно переоценить.

В "Liber Abaci" Фибоначчи приводит свою последовательность чисел как решение математической задачи - нахождение формулы размножения кроликов. Числовая последовательность такова: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 (далее до бесконечности).

На стр. 123- 124 данной рукописи, Фибоначчи поместил следующую задачу: "Некто поместил пару кроликов в некоем месте, огороженном со всех сторон стеной, чтобы узнать, сколько пар кроликов родится при этом в течении года, если природа кроликов такова, что через месяц пара кроликов производит на свет др. пару, а рождают кролики со второго месяца после своего рождения. "

Последовательность Фибоначчи имеет весьма любопытные особенности, не последняя из которых - почти постоянная взаимосвязь между числами.

Сумма любых двух соседних чисел равна следующему числу в последовательности. Например: 3 + 5 = 8; 5 + 8 = 13 и т. д.

Отношение любого числа последовательности к следующему приближается к 0,618 (после первых четырех чисел). Например: 1: 1 = 1; 1: 2 = 0,5; 2: 3 = 0,67; 3: 5 = 0,6; 5: 8 = 0,625; 8: 13 = 0,615; 13: 21 = 0,619 и т. д. Обратите внимание, как значение соотношений колеблется вокруг величины 0,618, причем размах флуктуаций постепенно сужается; а также на величины: 1,00; 0,5; 0,67.

Отношение любого числа к предыдущему приблизительно равно 1,618 (величина обратная 0,618). Например: 13: 8 = 1,625; 21: 13 = 1,615; 34: 21 = 1,619. Чем выше числа, тем более они приближаются к величине 0,618 и 1,618.

Отношение любого числа к следующему за ним через одно приближается к 0,382, а к предшествующему через одно - 2,618. Например: 13: 34 = 0,382; 34: 13 = 2,615.

Последовательность Фибоначчи содержит и другие любопытные соотношения, или коэффициент, но те, которые мы только что привели - самые важные и известные. Как мы уже подчеркивали выше, на самом деле Фибоначчи не является первооткрывателем своей последовательности. Дело в том, что коэффициент 1,618 или 0,618 был известен еще древнегреческим и древнеегипетским математикам, которые называли его "золотым коэффициентом" или "золотым сечением". Его следы мы находим в музыке, изобразительном искусстве, архитектуре и биологии. Греки использовали принцип "золотого сечения" при строительстве Парфенона, египтяне - Великой пирамиды в Гизе. Свойства "золотого коэффициента" были хорошо известны Пифагору, Платону и Леонардо да Винчи.

Пропорции чисел Фибоначчи дают ориентиры не только возможных уровней отката, но и указывают возможную величину хода в случае продолжения тенденции. Если после хода рынок откатывается, а затем продолжает ход в том же направлении, то в типичном случае величина продолженного хода может составить 1.618.

Остальные ответы

Золотое сечение и числа Фибоначчи

1.3. Золотое сечение и числа Фибоначчи

“Древние, - писал Г.Д.Гримм, - понимали пропорцию следующим образом: “Две части или две величины не могут быть. связаны между собой без посредства третьей. Достигается это. п ропорцией (аналогией), в которой из трех чисел. среднее так относится ко второму, как первое к среднему, а также второе к среднему, как среднее к первому” [50, с. 7]. Под пропорцией здесь понимается отношение частей целого между собой и с целым; очевидна особая роль среднего пропорционального. Оно содержит в себе, как считает М.А.Марутаев. “качественное обобщение, т.к. оно выражается одним числом, а не множеством” [89, с. 162]. Очевидно, что отдельные конкретные числа и отношения способны выражать не только количество, но и “качество”. Именно поэтому пропорции так существенны в выражении гармонии. Примером “качества”, представленного в отношении, является золотое число. Итак, гармония связана с числами; это ведет к пропорциям особого рода. Учение о золотом сечении возникло в результате тщательного исследования природы чисел. Считается, что деление отрезка в среднем и крайнем отношении впервые было осуществлено великим философом и геометром Древней Греции Пифагором, хотя по мнению Б.Л.Ван-дер-Вардена [26] Пифагор, возможно, позаимствовал его у египтян и вавилонян. Было показано, что отрезок единичной длины AB можно разделить на две части точкой С так, что отношение большей части ( CB=x ) к меньшей (AС=1-x) будет равняться отношению всего отрезка (AB=1) к его большей части (CB): С B /AC=(AC+CB)/CB, т.е. x /(1-x) =1/ x. Отсюда имеем алгебраическое выражение

x2 + x - 1 = 0.

Положительным корнем этого уравнения является (-1+ 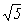)/2, так что отношение 1/ х в рассматриваемой пропорции равно числу

Такое деление Пифагор называл золотым делением или золотой пропорцией. Число 1,618 принято обозначать буквой Ф в честь древнегреческого скульптора Фидия, часто использующего золотую пропорцию в своих творениях. В соответствии с делением в среднем и крайнем отношении единичный отрезок АВ точкой С делится следующим образом:

1. 0,618 = 0,618. 0,382 = 1,618

0,382 + 0,618 = 1.

Письменные свидетельства, известные человечеству, о золотой пропорции впервые приводятся в ”Началах” Евклида (3 в. до н.э.). Евклид использовал вслед за пифагорейцами золотую пропорцию для построения правильных пятиугольников и десятиугольников. Пятиугольник, точнее пентаграмма, считался у пифагорейцев священным, поскольку эта фигура симметрична и в то же время воплощает в себе некоторую асимметрию - золотую пропорцию, полученную соотношением неравных частей отрезка. В силу своих особых свойств пентаграмма считалась у пифагорейцев символом жизни и здоровья. Существуют всего пять правильных многогранников: четырехгранник (тетраэдр), шестигранник (куб), восьмигранник (октаэдр), двенадцатигранник (додекаэдр) и двадцатигранник (икосаэдр). Все эти многогранники были известны древним грекам и получили название платоновых тел по имени Платона, впервые их систематически описавшим. Каждое из них символизировало какое-то из 5 “начал” или “стихий”: тетраэдр - тело огня, октаэдр - тело воздуха, гексаэдр (куб) - тело земли, икосаэдр - тело воды, - додекаэдр - тело мира (вселенской души, эфира или разума). В средние века И.Кеплер (1571-1630) представил модель Солнечной системы в форме последовательности вложенных друг в друга политонов ( платоновых тел). Евклидом была показана возможность построения всех правильных многогранников на основе деления отрезка в среднем и крайнем отношении [73]. В последствии золотым делением занимались Гипоксил (2 в. до н.э.), Папп (3 в. до н.э.), Дж. Компано из Наварры (13 в .). Как считает Э.М.Сороко [121], термин “золотое сечение” происходит от Птолемея. Закрепилось это обозначение и стало популярным благодаря Леонардо да Винчи (1452-1519), который часто его использовал.

В 1202 г. вышло в свет сочинение " Liber abaci " итальянского математика Леонардо Пизанского (1180-1240), известного, однако, больше как Фибоначчи. В книге излагается множество задач. Одна из них ставится и решается следующим образом.

“Сколько пар кроликов в один год от одной пары рождается? Некто поместил пару кроликов в некоем месте, огороженном со всех сторон стеной, чтобы узнать, сколько пар кроликов родится в течение года, если природа кроликов такова, что через месяц пара кроликов производит на свет другую пару, а рождают кролики со второго месяца своего рождения. Так как 1-я пара в 1-м месяце дает потомство, удвой, и в этом месяце окажется две пары; из них одна пара, а именно первая, рождает и в следующем месяце, так что во втором месяце окажется 3 пары; из них в следующем месяце 2 пары будут давать потомство, так что в третьем месяце родится еще 2 пары кроликов, и число пар кроликов в этом месяце достигнет 5”, и т.д. Свое решение задачи Фибоначчи представляет так: “Мы складываем первое число со вторым, т.е. 1 и 2; и второе с третьим; и третье с четвертым; и так одно за другим, пока не сложим десятое с одиннадцатым, т.е. 144 и 233; и мы получим общее число кроликов, т.е. 377; и так можно делать по порядку до бесконечного числа месяцев”. Обозначив число кроликов в n-ый месяц через fn. а в следующие месяцы - fn+1. fn+2 и т.д. последовательность чисел ряда Фибоначчи можно представить формулой

fn+2 = fn + fn+1.

И.Кеплер установил, что fn+1 / fn ® Ф. а Р.Симпсон (1687-1768) строго доказал, что 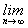fn+1/ fn=Ф. В 1843 г. Ж.Бине нашел формулу, определяющую n-член фибоначчиевой последовательности,

fn =( F -1/(-5) n ) / .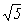

Позднее было установлено, что не только классический ряд Фибоначчи, но и всякий ряд с рекуррентным свойством с любыми начальными членами a и b порождает последовательность a+b. a+2b, 2a+3b, 3a+5b, 5a+8b и т.д. отношение соседних членов которой по мере удаления от начала стремится к величине Ф =1,618. Примером такой последовательности может служить ряд Люка: 1, 3, 4, 7, 11, 18, 29, 47 и т.д.

С золотым сечением и числами Фибоначчи связаны целые области в культуре, науке и практической деятельности человека с древности до наших дней. Известно [121], что многие египетские архитектурные памятники построены на основе пропорции золотого сечения и чисел Фибоначчи. Например, с числами 55, 89, 144 связаны не только внешние пропорции пирамид, но и внутренние - зал фараона (пирамиды Хеопса, Хефрена и Микерина ). Золотая или божественная пропорция, являясь чисто математическим соотношением, получила широкое применение в творениях скульпторов и архитектуре Древней Греции. У древних греков все сколько-нибудь крупные архитектурные сооружения (храмы, стадионы, амфитеатры) построены таким образом, что в них многообразно представлена золотая пропорция. Фригийские гробницы и античный Парфенон, театр в Эпидавре и театр Диониса в Афинах - яркие образцы ваяния и зодчества, исполненные глубокой гармонии на основе золотого сечения. Если в Древнем Египте закон золотого деления используется спорадически, то в Древней Греции - постоянно. В средние века интерес к золотому сечению пропал и свойства этой пропорции были практически забыты. Влечение к “божественному сечению” резко возросло в эпоху Ренессанса. Известный ученый, монах-минорит францисканского ордена Л. Пачоли ди Борго посвятил этой пропорции восторженную книгу “Божественная пропорция” (1509 г.). В этой книге [245] систематически излагались 12 различных свойств гармонической пропорции. Характеризуя эти свойства, Пачолли пользовался весьма сильными эпитетами: “исключительное”, “превосходное”, “замечательное”, “почти сверхъестественное” и т.д. Раскрывая данную пропорцию в качестве универсального отношения и в природе, и в искусстве как совершенство красоты, он называл ее “божественной” и склонен был ее рассматривать как “орудие мышления”, “эстетический закон”, как “принцип мира и природы”. Эта книга сопровождалась прекрасными иллюстрациями Л. да Винчи, который “закрепил” за золотой пропорцией обозначение “золотое сечение” ( sectio aurea ). Вслед за Л. Пачолли И.Кеплер не менее восторженно говорит о золотом сечении, называя его божественным сечением ( sectio divina ). Он писал: “Геометрия владеет двумя сокровищами: одно из них - это теорема Пифагора, а другое - деление отрезка в среднем и крайнем отношении. Первое можно сравнить с мерой золота, второе же больше напоминает драгоценный камень” [217, c. 23]. Имеются свидетельства, что И.Кеплер одним из первых обратил внимание на проявления золотого сечения в ботанике. Особенно большой интерес к золотой пропорции проявили ученые, зодчие и художники 15-16 веков, его широко применяли в геометрии, искусстве и особенно в архитектуре. В произведениях Браманте. Л. да Винчи, Рафаэля, Джорджане. Тициана, Микельанджело и других проявляется строгая размерность и гармоничность сюжета, подчиняющаяся золотому сечению. Знаменитые итальянские мастера Страдивариус, Амати и др. применяли геометрию пентаграммы и золотое сечение в очертаниях своих скрипок. Шедеврами древнерусской архитектуры являются церковь Покрова на Нерли (12 в.), собор Василия Блаженного (16 в.), церковь Вознесения села Коломенское под Москвой (16 в.) и др.; в формах этих сооружений использованы элементы золотого сечения [27].

После эпохи Ренессанса интерес к золотому сечению на значительное время прервался и в течение более 200 лет эта пропорция была предана забвению. Лишь во второй половине 19 - начале 20 в.в. появились публикации, в которых золотое сечение впервые было установлено во многих явлениях и закономерностях биологических объектов. Среди них видное место занимают труды А.Цейзинга [296, 297]. Цейзинг рассматривал золотое сечение как основной морфологический закон в природе и искусстве. Он показал, что этот закон проявляется в пропорциях тела человека и в телах красивых животных. Г.Т.Фехнером [200] была установлена связь между психофизическим восприятием человека и “золотыми” формами предметов. Т.Кук [41] уделяет большое внимание изучению роли логарифмической спирали в растительных и животных объектах. Им установлено, что феномен роста в биологических объектах связан со спиралями золотого сечения. О значении золотой пропорции в природе и искусстве пишут Г.Тимеринг [125], Г.Д.Грим [50] и М.Гика [41], которые приводят многочисленные примеры проявлений золотого сечения в явлениях природы и различных прикладных искусствах. Интересные исследования об использовании золотой пропорции в шедеврах музыки, живописи и поэзии были проведены в в России и СССР Э.К.Розеновым [109], Л.Сабанеевым [112], Г.В.Церетели [154], М.А.Марутаевым [89], Н.А.Васютинским [27]. Выдающийся советский режиссер С.М.Эйзенштейн [168] занимался исследованием золотого сечения в кино. Он сознательно использовал золотое сечение при структурном построении фильма “Броненосец Потемкин”, а также при формировании отдельных кульминационных кадров фильма. Большое количество исследований посвящено проявлению золотого сечения в шедеврах древних зодчих и в современной архитектуре [110, 161 и др.]. А.Б.Рыбаков [110] считает, что во многих архитектурных шедеврах древности золотое сечение проявляется по антропологическим признакам, т.к. золотая пропорция четко прослеживается в членении тела человека. Интересно отметить, что установлена связь старинных мер длины (локоть, ступня, различные сажени и т.д.) с золотым сечением. Выдающийся французский архитектор Ле Корбюзье положил золотое сечение в основу своей теории гармонизации в строительстве, известную под названием система “ Модулор ” [82]. В этой системе Ле Корбюзье объединил существующие представления о пропорциях человеческого тела с отношением золотой пропорции.

После некоторого ослабления внимания к золотому сечению в середине нынешнего столетия во второй его половине резко возрос интерес к этой пропорции со стороны многих ученых в различных отраслях знаний. В США начал регулярно выходить журнал “ The Fibonacci Quarterly ”. В СССР публикуется ряд работ, относящихся к разнообразным областям науки: поиску экстремумов унимодальных функций [128], математическом описании принципов оптимизации живых систем [22], организации Солнечной системы [25], теории развития этнических культур [23], лечению некоторых заболеваний человека [54, 118, 124], в экономике [28]. Н.Н.Воробьев [38] показал связь золотого сечения с теорией возвратных рядов, комбинаторной математикой, теорией чисел, геометрией, теорией поисков. Настоящий “взрыв” исследований по проблеме золотого сечения в нашей стране приходится на последние 10-15 лет. В эти годы в СССР и странах СНГ появились крупные работы в различных отраслях знаний, где золотая пропорц ия и ее закономерности использованы как своеобразный методологический принцип, лежащий в основе анализа технических и природных систем, их структурной гармонии.

А.П.Стахов [122] развивает направление по приложению обобщенных золотых сечений и p-чисел Фибоначчи к решению задач математической теории измерений и использованию нетрадиционных методов в теории кодирования информации. Геометрическая интерпретация рекуррентного соотношения для р-чисел Фибоначчи может быть получена, если мы разделим отрезок АВ точкой С в таком отношении, чтобы AB/ CB=x. а CB/ ACp = xp. Значение искомого отношения АВ/ СВ сводится к решению алгебраического уравнения

xp+1+ xp - 1 = 0.

Ниже приведены приближенные значения золотых р-пропорций. соответствующие начальным значениям р.

Золотое сечение и Золотая пропорция

Принято считать, что объекты, содержащие в себе «золотое сечение», воспринимаются людьми как наиболее гармоничные, пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона якобы свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании. Швейцарский архитектор Ле Корбюзье «нашёл», что в рельефе из храма фараона Сети I в Абидосе и в рельефе, изображающем фараона Рамзеса, пропорции фигур соответствуют величинам золотого деления. Зодчий Хесира, изображённый на рельефе деревянной доски из гробницы его имени, держит в руках измерительные инструменты, в которых зафиксированы пропорции золотого деления.

Ко всем этим утверждениям следует относиться с осторожностью, поскольку во многих случаях это может оказаться результатом подгонки или совпадения.

Золотое сечение в искусстве

Начиная с Леонардо да Винчи, многие художники сознательно использовали пропорции «золотого сечения». Размеры холста для картин художники нередко выбирали в соответстии с этой пропорцией.

Так, известно, что С. Эйзенштейн искусственно построил фильм Броненосец Потёмкин по правилам «золотого сечения». Он разбил ленту на пять частей. В первых трёх действие разворачивается на корабле. В двух последних — в Одессе, где разворачивается восстание. Этот переход в город происходит точно в точке золотого сечения. Да и в каждой части есть свой перелом, происходящий по закону золотого сечения.

В кадре, сцене, эпизоде происходит некий скачок в развитии темы: сюжета, настроения. Эйзенштейн считал, что так как такой переход близок к точке золотого сечения, он воспринимается как наиболее закономерный и естественный.

Другим примером использования правила «Золотого сечения» в киноискусстве — расположение основных компонентов кадра в особых точках — «зрительных центрах». Часто используются четыре точки, расположенные на расстоянии 3/8 и 5/8 от соответствующих краёв плоскости.

Золотые пропорции в строении молекулы ДНК. Все сведения о физиологических особенностях живых существ хранятся в микроскопической молекуле ДНК, строение которой также содержит в себе закон золотой пропорции. Молекула ДНК состоит из двух вертикально переплетенных между собой спиралей. Длина каждой из этих спиралей составляет 34 ангстрема, ширина 21 ангстрема. (1 ангстрем - одна стомиллионная доля сантиметра).

Так вот 21 и 34 - это цифры, следующие друг за другом в последовательности чисел Фибоначчи, то есть соотношение длины и ширины логарифмической спирали молекулы ДНК несет в себе формулу золотого сечения 1:1,618.

Золотое сечение в строении снежинок

Золотое сечение присутствует в строении всех кристаллов, но большинство кристаллов микроскопически малы, так что мы не можем разглядеть их невооруженным глазом. Однако снежинки, также представляющие собой водные кристаллы, вполне доступны нашему взору. Все изысканной красоты фигуры, которые образуют снежинки, все оси, окружности и геометрические фигуры в снежинках также всегда без исключений построены по совершенной четкой формуле золотого сечения.

Золотые пропорции в космическом пространстве

Во Вселенной все известные человечеству галактики и все тела в них существуют в форме спирали, соответствующей формуле золотого сечения.

Строение всех встречающихся в природе живых организмов и неживых объектов, не имеющих никакой связи и подобия между собой, спланировано по определенной математической формуле. Это является самым ярким доказательством их осознанной сотворенности согласно некоему проекту, замыслу. Формула золотого сечения и золотые пропорции очень хорошо известны всем людям искусства, ибо это главные правила эстетики. Любое произведение искусства, спроектированное в точном соответствии с пропорциями золотого сечения, являет собой совершенную эстетическую форму.

Вне сомнения, что все в нашем мире, в окружающей нас жизни сотворено Всевышним Господом без какого либо подобия. Тогда как люди только копируют и подражают примерам, существующим в природе, которые Он сотворил.

Мы лишь воспроизводим с большей или меньшей степенью мастерства подобия совершенства форм жизни, что окружают нас повсеместно.