


 Рейтинг: 4.3/5.0 (1918 проголосовавших)
Рейтинг: 4.3/5.0 (1918 проголосовавших)Категория: Windows: Математика
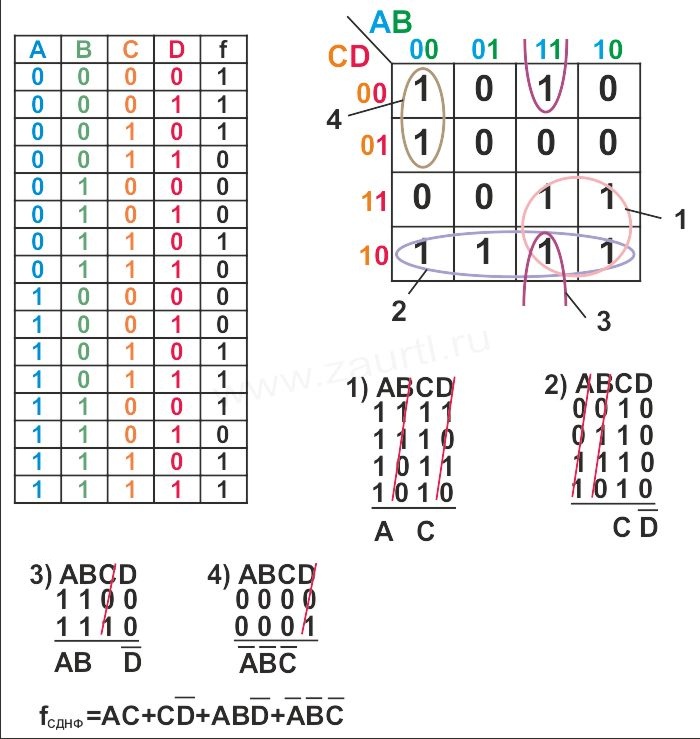
Такая таблица называется таблица истинности.
Алгебраическая форма представления булевых функций используется для минимизации (упрощения формул) и для построения логических схем. Существует две формы алгебраических функций – дизъюнктивная и конъюнктивная. Дизъюнктивная нормальная форма представляет собой сумму элементарных произведений аргументов, например
Если каждое слагаемое содержит все аргументы или их отрицания, то получаем совершенную дизъюнктивную нормальную форму (СДФН), например
Совершенная конъюнктивная нормальная форма (СКНФ) представляет собой логическое произведение элементарных логических сумм, причем каждая сумма содержит все аргументы или их отрицания, например
Для перехода от таблицы истинности к СДНФ учитываются только те состояния, для которых функция равна 1. Для каждого такого состояния записывается элементарное произведение всех аргументов. Если аргумент имеет значение "0", то записывается его отрицание. Для приведенного примера СДНФ имеет вид
Для перехода от таблицы истинности к СДНФ учитываются только те состояния, для которых функция равна "0". Для каждого такого состояния записывается элементарная сумма аргументов. Если аргумент имеет значение "1", то пишется его отрицание. Для приведенного примера СКНФ имеет вид
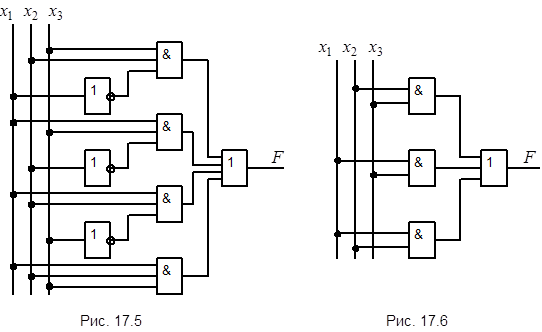
На основании полученных формул (17.4) или (17.5) можно построить логическую схему, состоящую из элементов "ИЛИ", "И", "НЕ". Для функции (17.4) сначала изображаются инверторы, затем ячейки "И" и потом ячейки "ИЛИ" (см. рис. 17.5).
Схемы рис. 17.4 и рис. 17.5 содержат все типы логических элементов. При проектировании всегда стремятся номенклатуру элементов. В связи с этим созданы логические элементы, способные выполнить простейшую функцию двух аргументов "ИЛИ-НЕ", а также "И-НЕ". С помощью каждого из этих элементов можно выразить все основные операции булевой алгебры, а значит реализовать любую логическую функцию. Покажем это.
Для элемента "ИЛИ-НЕ"
Карты Карно - это графическое представление операций попарного неполного склеивания и элементарного поглощения.
Карты Карно рассматриваются как перестроенная соответствующим образом таблица истинности функции.
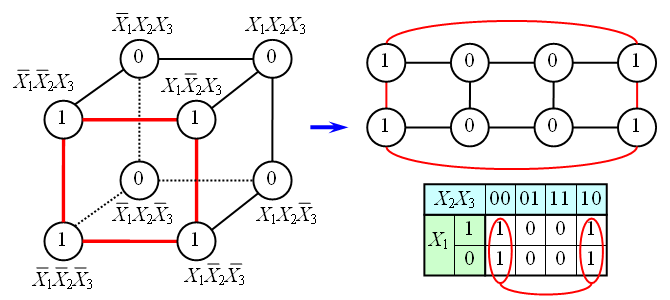
Карты Карно - определенная плоская развертка n-мерного булева куба.
Строится таблица истинности функции определенным образом. Каждая клетка таблицы соответствует вполне определенной вершине булева куба. Нулевые значения не записываются.
Карта Карно для функции 4-х переменных:
Карта Карно рассматривается как поверхность фигуры под названием тор ("бублик").
p-клетки - клетки карты Карно, соответствующие единичному значению функции.
Соседние наборы - наборы, которые различаются только одним аргументом (одной орбитой).
Любой паре соседних наборов в Карте Карно соответствуют соседние клетки.
Две соседние p-клетки на карте Карно дают импликанту первого ранга. Например, клетки 1100 и 1101 отличаются только значением переменной x3. следовательно, они дают импликанту  1
1 2
2 4.
4.
Две соседние импликанты первого ранга образуют импликанту второго ранга .
На этой карте соседние клетки образуют импликанты a,b,c,d,e. При этом импликанты a и b являются соседними, поэтому они образуют импликанту второго ранга.
Если функция имеет 5 переменных, то рисуются 2 Карты Карно: для x5 =0 и для x5 =1. Если 6 переменных - 4 Карты, так чтобы в соседних картах соседние клетки имели одинаковые координаты:
Соседние p-клетки, соответствующие импликанте образуют компактную группу.
Количество p-клеток в компактной группе является степенью двойки.
Задача минимизации переключательной функции с помощью карт Карно заключается в нахождении импликант высшего ранга (соответствующих компактным группам наибольшей размерности), покрывающих p-клетки функции наилучшим образом.
Если на картах Карно выделить все компактные группы наибольшей размерности, то дизъюнкция соответствующих конъюнкций даст СкДНФ.
Пример минимизации функции 4-х переменных методом Карт КарноТаблица истинности — это таблица, которая описывает логическую функцию. Логическая функция здесь — это функция, у которой значения переменных и значение самой функции выражают истинность. Например, они принимают значения «истина» либо «ложь» (true либо false, 1 либо 0).
Таблицы истинности применяются для определения значения какого-либо высказывания для всех возможных случаев значений истинности высказываний, которые его составляют. Количество всех существующих комбинаций в таблице находится по формуле N=2*n; где N - общее количество возможных комбинаций, n - число входных переменных. Таблицы истинности нередко используются в цифровой технике и булевой алгебре, чтобы описать работу логических схем.
Таблицы истинности для основных функцийПримеры. конъюнкция - 1&0=0, импликация - 1>0=0.
Последовательность построения (составления) таблицы истинности:
Таким образом, можно составить (построить) таблицу истинности самостоятельно.
Составить таблицу истинности онлайнЗаполните поле ввода и нажмите OK. T - истина, F - ложь. Рекомендуем добавить страницу в закладки или сохранить в социальной сети.
Первый метод построения сокращенной ДНФ булевой функции основан на следующей теореме.
Теорема (Квайна). Чтобы получить сокращенную ДНФ булевой функции из ее совершенной ДНФ, надо выполнить всевозможные неполные склеивания соседних конъюнкций, а затем всевозможные поглощения конъюнкций.
Опираясь на теорему Квайна, МакКласки сформулировал алгоритм, который организует построение сокращенной ДНФ более эффективно, чем это предложено в теореме.
Во-первых, конъюнкции в алгоритме представляются булевыми и троичными векторами, что делает вычисления более простыми и более приспособленными для компьютерной реализации.
Во-вторых, соседние векторы отличаются по весу (числу единичных компонент) ровно на единицу. Поэтому в алгоритме не проверяются на возможность склеивания векторы, чьи веса равны или отличаются более чем на единицу.
В-третьих, соседние вектора поглощаются результатом их склеивания. Поэтому отметка склеиваемых соседей (но не вычеркивание их, так как один и тот же вектор может быть соседом нескольким векторам) позволяет свести поглощение к выписыванию неотмеченных векторов.
Алгоритм Квайна –МакКласки.
Начало. Задана совершенная ДНФ булевой функции.
Шаг 1. Построим список всех точек функции (булевых векторов) и упорядочим их по неубыванию числа единиц – веса.
Шаг 2. Разобьем список на подмножества (классы) векторов одинакового веса. Обозначим через Ci класс векторов веса i.
Шаг 3. Выполним неполные склеивания всех соседних векторов классов Ci и Ci+1. i = 0,1, …, n-1. Участвующие в склеивании векторы (α и β) отметим, а полученные векторы (γ) занесем в новый список и приведем в нем подобные.
Шаг 4. Если новый список векторов не пуст, возвратимся с ним на шаг 2 (заметим, что троичные векторы списка оказываются уже упорядоченными по числу единиц).
Конец. Выписав из всех списков неотмеченные векторы, получим множество всех максимальных интервалов, оно задает сокращенную ДНФ исходной функции.
Пример. Продемонстрируем выполнение алгоритма, для наглядности сопровождая его шаги матрицами Грея.
Начало. Задана совершенная ДНФ булевой функции:
СовДНФ = a b c d  a b c d
a b c d  a bcd
a bcd  a b c d
a b c d  abcd
abcd abc d
abc d  a b cd.
a b cd.
Шаги 1, 2. Совершенную ДНФ представляем списком точек, упорядочиваем их по весу и разбиваем на классы.
Шаг 3. Выполняя неполные склеивания векторов из классов C2 и C3. а затем C3 и C4. и отмечая в упорядоченном списке 0 склеиваемые векторы символом *, получаем список 1 – список интервалов, состоящих из двух точек. Справа в новом списке указаны номера векторов – участников склеивания. Интервалы списка изображены на двух матрицах Грея.
Шаг 4. Список 1 не пуст, поэтому идем на шаг 2 (так как склеивания производились в строгом порядке ''сверху вниз'', векторы в новом списке уже упорядочены по весу).
Шаги 2, 3. Разбиваем полученный список на классы C2. C3. Выполняя склеивания векторов из классов C2 и C3. получаем список интервалов, состоящих из четырех точек (список 2). Приводим в нем подобные.
Шаг 4. Список 2 не пуст, но дальнейшее склеивание невозможно, поэтому список 3 окажется пустым, идем на конец.
Конец. Выписываем из всех списков неотмеченные векторы. Они задают сокращенную ДНФ:
Упрощение логических выражений с помощью тождеств основывается на интуитивных решениях и представляет большие трудности, особенно при большом числе переменных. При этом бывает трудно оценить, является ли полученное выражение простейшим или возможны дальнейшие упрощения.
Минимизацию логических функций можно провести, используя диаграммы Вейча (или аналогичный метод карт Карно). Диаграмма Вейча для функции F четырех переменных А, В, С, D представлена на рис. 4.13. Каждая из переменных принимает два значения, т. е. возможны  комбинаций входных функций. Диаграмма Вейча содержит 16 клеток, каждая из которых соответствует одной из 16 возможных комбинаций входных переменных. На полях диаграммы обозначены значения каждой переменной. Диаграмма состоит
комбинаций входных функций. Диаграмма Вейча содержит 16 клеток, каждая из которых соответствует одной из 16 возможных комбинаций входных переменных. На полях диаграммы обозначены значения каждой переменной. Диаграмма состоит  четырех строк и четырех столбцов.
четырех строк и четырех столбцов.
Рассмотрим минимизацию логической функции на примере.
Дано: Упростить функцию  .
.
Решение разбиваем на четыре операции.
1. Преобразование исходного выражения. При преобразовании необходимо раскрыть скобки и исключить знаки инверсии над комбинацией переменных. Последнее осуществляется с помощью формул де Моргана. Получим
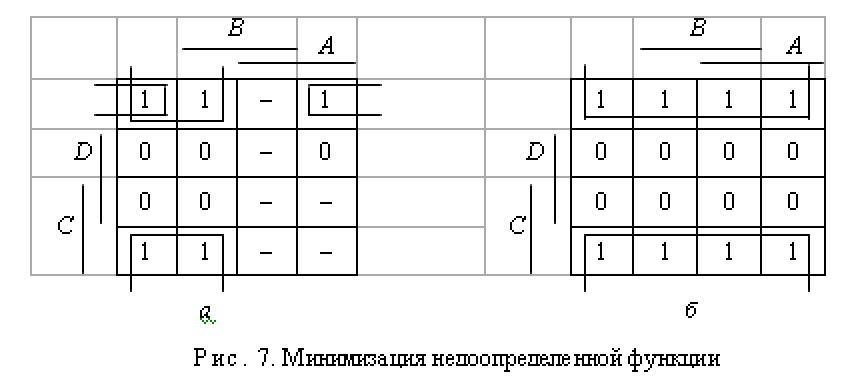
2. Заполнение диаграммы Вейча проводим при наличии в полученном выражении соответствующих комбинаций входных переменных, эти клетки обозначаются знаком 1 (рис. 4.14,а). Если слагаемое не содержит одного или нескольких переменных, то должны заполняться клетки, соответствующие и прямому, и инверсному значениям отсутствующей переменной.
Рис. 4.13. Диаграмма Вейча для функции четырех переменных
Рис. 4.14. К минимизации схемы логического комбинационного устройства: а — диаграмма Вейча; б — схема на элементах 
Например:  . Заполняются клетки ABCD и ABCD.
. Заполняются клетки ABCD и ABCD.
3. Производится «склейка» клеток. Можно склеить (т. е. объединить, лак показано на рис. 4.14, я) целую заполненную строку, целый столбец, полстроки или полстолбца. Можно склеить соседние строки, столбцы, полустроки и полустолбцы. Склейки можно располагать через границы диаграммы Вейча, т. е. объединяя нижиий и верхний, правый и левый края. Одиа склейка может накладываться на другую. Склейки содержат 2, 4, 8 клеток.
Для успешной минимизации нужно расположить на таблице минимальное количество склеек, каждая из которых содержит наибольшее количество клеток.
Склейки для логической функции F показаны на рис. 4.14, а.
4. Расшифровка склеек. Каждая склейка представлена в виде конъюнкции переменных. Второй столбец на диаграмме рис. 4.14, я расшифровывается как АС, так как он охватывает и прямые, и инверсные значения переменных В и D, т. е. от В до D не зависит. Склейка в правой верхней части таблицы расшифровывается как АВ, а склейка из двух клеток в четвертом столбце соответствует ACD. Результат минимизации:
На рис.  приведена схема на элементах
приведена схема на элементах  , реализующая функцию F. При построении схемы использованы стандартные решения, приведенные на рис. 4.11.
, реализующая функцию F. При построении схемы использованы стандартные решения, приведенные на рис. 4.11.
Процедура минимизации функций с помощью диаграмм Вейча очень проста, и ее использование заменяет путь сложных преобразований с помощью тождеств. С помощью диаграмм Вейча можно минимизировать и функции трех переменных, при этом  , т. е. из диаграммы исключают первую и четвертую строки, диаграмма содержит только восемь клеток.
, т. е. из диаграммы исключают первую и четвертую строки, диаграмма содержит только восемь клеток.
Правила склеек не изменяются.
Диаграмма Вейча функции двух переменных содержит четыре клетки.
Переключательные функции являются математическими моделями некоторых реальных электронных цифровых схем. Для того чтобы синтезировать наиболее оптимальное цифровое устройство (например, имеющее минимальные аппаратные затраты), математическую модель этого устройства, представленную в виде СДНФ или СКНФ, преобразуют к соответствующему виду с использованием приведенных выше законов алгебры логики. Преобразование СДНФ или СКНФ логической функции к минимальному виду аналитической записи называется процессом минимизации ФАЛ. Однако результат минимизации функции с помощью законов и тождественных преобразований булевой алгебры во многом зависит от опыта разработчика и не всегда является очевидным. Поэтому разработан ряд алгоритмов, формализующих и автоматизирующих подобные преобразования.
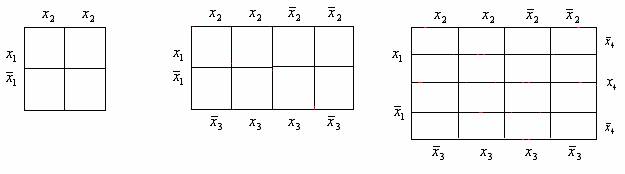
Рассмотрим один из алгоритмов минимизации, предложенный американский ученым Вейчем. Вейч предложил специальные диаграммы-карты. в которые можно записать все конституенты единицы, входящие в СДНФ (конституенты нуля, входящие в СКНФ) той или иной булевой функции. На рис. 1.2 в качестве примера приведены диаграммы для минимизаций функций двух, трех и четырех переменных соответственно.
Рис. 1.2.Диаграммы Вейча для функций 2-х, 3-х и 4-х переменных.
Каждой клетке диаграммы в случае минимизации СДНФ соответствует определенная конситуента единицы. Метод минимизации с помощью диаграмм Вейча заключается в следующем. Конституенты единицы, входящие в СДНФ булевой функции, заносятся в соответствующие клетки диаграммы. Удобно наличие соответствующей конституенты единицы изображать в клетке диаграммы цифрой 1, а отсутствие - 0. Все диаграммы построены таким образом, что рядом расположенные единицы по горизонтали или вертикали склеиваются между собой в соответствии с законом склеивания алгебры логики. Одну и ту же конституенту единицы можно использовать для склеивания с несколькими другими конституентами единицы с целью получения наиболее простого окончательного выражения. Цель всех операций - получить как можно меньшее число прямоугольников (в том числе квадратов), чтобы число членов СДНФ уменьшилось, получив в итоге МДНФ.
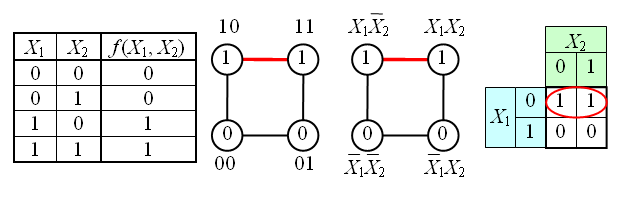
Формировать прямоугольники можно только при включении в них хотя бы одного нового члена. Склеивание можно осуществлять и путем замыкания крайних ребер в «бочку». Таким образом, полученная диаграмма Вейча геометрически образует цилиндр. На рис. 1.3 приведены некоторые правила склеивания конституент единицы для функций 2-х и 3-х переменных.
Поскольку для ФАЛ трех переменных диаграмма представляет как бы развертку цилиндра, разрезанного по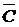 , поэтому единицы, расположенные по краям диаграммы (например, как это изображено на рис. 1.3 ) считаются расположенными рядом.
, поэтому единицы, расположенные по краям диаграммы (например, как это изображено на рис. 1.3 ) считаются расположенными рядом.
Метод минимизации СДНФ с помощью диаграмм Вейча включает в себя следующие шаги:
производится занесение в соответствующую диаграмму конституент единицы, входящих в СДНФ минимизируемой функции;находится искомая минимальная дизъюнктивная нормальная форма (МДНФ) ФАЛ выбором минимальной совокупности простых импликант, покрывающей все конституенты единицы диаграммы.
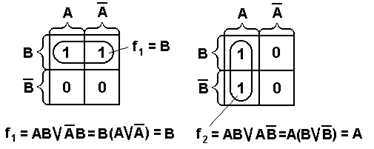
Рис. 1.3. Примеры для иллюстрации правил склеивания.
В качестве примера найдем МДНФ функции, заданной таблицей 1.3. Диаграмма Вейча этой функции представлена на рис. 1.4. Из рисунка видно, что в результате склеивания образовались две простые импликанты: 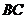 и
и 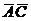 . Импликанта
. Импликанта 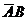 участвует в склеивании с конъюнкциями
участвует в склеивании с конъюнкциями 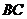 и
и 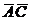 и поэтому не является простой. Таким образом, полученная МДНФ имеет вид
и поэтому не является простой. Таким образом, полученная МДНФ имеет вид 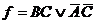 . В истинности полученного выражения можно убедиться путем подстановки всех наборов переменных А, В и С .
. В истинности полученного выражения можно убедиться путем подстановки всех наборов переменных А, В и С .
Рис. 1.4.Пример минимизации функции, заданной таблицей 1.3.
Аналогом диаграмм Вейча являются карты Карно. Они позволяют изображать на плоскости прямоугольника конституенты единицы (нуля) для ФАЛ более четырех переменных. В отличие от диаграмм Вейча, в которых отдельным строкам и столбцам соответствуют отдельные переменные, в картах Карно им можно присваивать значения нескольких переменных. При этом должны быть представлены все возможные комбинации этих переменных, например: 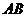 ,
, 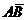 ,
, 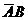 и
и 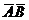 . Таким образом, общее количество переменных минимизируемой с помощью карты Карно ФАЛ может быть больше, чем в случае использования диаграмм Вейча. Сам процесс минимизации аналогичен описанному на примере диаграмм Вейча.
. Таким образом, общее количество переменных минимизируемой с помощью карты Карно ФАЛ может быть больше, чем в случае использования диаграмм Вейча. Сам процесс минимизации аналогичен описанному на примере диаграмм Вейча.
Минимизация ФАЛ методом диаграмм Вейча и карт Карно в силу своей наглядности широко используется при ручном процессе минимизации логических функций от небольшого количества переменных, обычно не превышающего пяти. В случае, когда количество переменных больше, необходимо использовать методы, характеризующиеся однозначностью алгоритма, что позволяет автоматизировать процесс минимизации на ЭВМ. Одним из таких методов является метод Квайна и Мак-Класки. Суть метода состоит в следующем:
все конституенты единицы, записанные в виде двоичных кодов, разбиваются на группы, содержащие одинаковое количество единиц;если среди выделенных столбцов существуют такие, которые покрываются базисными импликантами из ядра функции, то они считаются уже учтенными в записи МДНФ, если же выделенные столбцы базисными импликантами не покрываются, то в МДНФ записываются импликанты соответствующих столбцов с минимальным количесвом переменных.
Рассмотрим пример минимизации функции f. заданной таблицей 1.3 методом Квайна и Мак-Класски. Функция принимает единичные значения при следующих значениях переменных А. В и С - 000, 010, 011, 111, которые и образуют конституенты единицы. Эти конституенты можно записать в четыре группы по количеству в них единиц:
группа 0: 000 *;
группа 1: 010 *;
группа 2: 011 *;
группа 3: 111 *.
Осуществим склеивание конституент из соседних групп. Те конституенты, которые удается склеить, пометим звездочкой. Результатом склеивания являются импликанты, которые аналогично записываются в группы по количеству в них единиц. Вместо несовпадающих разрядов в записи импликант проставляются прочерки:
группа 1: 0-0;
группа 2: 01-;
группа 3: -11.
Дальнейшее склеивание соседних импликант возможно только при наличии прочерка в одинаковых позициях. В нашем примере это условие не выполняется и, поэтому, образованные импликанты являются простыми. Из полученных простых импликант составляется импликантная матрица, в первой строке которой записываются все конституенты единицы, а в первом столбце – все простые импликанты. Звездочкой отмечаются все пересечения строк и столбцов, в которых импликанты покрывают конституенты единицы.
Рейтинг пользователей:



 / 1
/ 1
Худший Лучший
Минимизация ФАЛ
Совершенно нормальные формы хотя и дают однозначные представления функции, но являются очень громоздкими. Реализация СНФ программно или схемотехнически является избыточной, что ведет к увеличению программного кода, поэтому существуют методы упрощения логической записи – минимизации.
Определение: Преобразование логических функций с целью упрощения их аналитического представления называются минимизацией.
Существуют два направления минимизации:
1. Кратчайшая форма записи (цель – минимизировать ранг каждого терма). При этом получаются кратчайшие формы КДНФ, ККНФ, КПНФ.
2. Получение минимальной формы записи (цель – получение минимального числа символов для записи всей функции сразу).
При этом следует учесть, что ни один из способов минимизации не универсален!
Существуют различные методы минимизации:
1. Метод непосредственных преобразований логических функций. (1.1)
При применении данного метода: а) Записываются ДСНФ логических функций б) Форма преобразуется и упрощается с использованием аксиом алгебры логики.
При этом, в частности, выявляются в исходном ДСНФ так называемые соседние min-термы, в которых есть по одной не совпадающей переменной.
По отношению к соседним min-термам применяется закон склейки, значит ранг min-терма понижается на единицу.
Определение: Min-термы, образованные при склеивании называются импликантами.
Полученные после склейки импликанты по возможности склеивают до тех пор, пока склеивание становится невозможным.
Определение: Несклеивающиеся импликанты называются прослойками.
Определение: Формула, состоящая из простых импликант – тупиковая.
|[pic] |[pic] |[pic] |[pic] |[pic] |
|0 |0 |0 |1 | |
|0 |0 |1 |1 | |
|0 |1 |0 |1 | |
Если в процессе склейки образуется форма R, содержащая члены вида [pic] и
Метод неопределенных коэффициентов. (1.2)
Суть метода состоит в преобразовании ДСНФ в МДНФ.
На основании теоремы Жигалкина любую ФАЛ можно представить в виде
(рассмотрим на примере трех переменных):
Алгоритм определения коэффициентов:
1. Исходное уравнение разбить на систему уравнений, равных числу строк в таблице истинности.
2. Напротив каждого выражения поставить соответствующее значение функции.
3. Выбрать строку, в которой значение функции [pic]и приравнять все [pic] к нулю.
4. Просмотреть строки, где функция имеет единичное значение, и вычеркнуть все коэффициенты, встречающиеся в нулевых строках.
5. Проанализировать оставшиеся коэффициенты в единичных строках.
6. Используя правило, что дизъюнкция равна 1 если хотя бы один из [pic], выбрать min-термы минимального ранга. Причем отдавать предпочтение коэффициентам, встречающимся в нескольких уравнениях одновременно.
7. Записать исходный вид функции.
Метод неопределенных коэффициентов применим для дизъюнктивной формы и непригоден для конъюнктивной.
| |[pic] |[pic] |[pic] |[pic] |[pic] |[pic] |[pic] |[pic] |
|0 |0 |0 |0 |00 |00 |00 |000 |1 |
|1 |0 |0 |1 |00 |01 |01 |001 |0 |
|2 |0 |1 |0 |01 |00 |10 |010 |1 |
|3 |0 |1 |1 |01 |01 |11 |011 |0 |
|4 |1 |0 |0 |10 |10 |00 |100 |1 |
|5 |1 |0 |1 |10 |11 |01 |101 |0 |
|6 |1 |1 |0 |11 |10 |10 |110 |0 |
Итак, получим [pic]
Метод Квайна (1.3)
Суть метода сводится к тому, чтобы преобразовать ДСНФ в МДНФ. Задачи минимизации по методу Квайна состоит в попарном сравнении импликант, входящих в ДСНФ с целью выявления возможности склеивания по какой-то пременной так:
Таким образом, можно понизить ранг термов. Процедура производится до тех пор, пока не остается ни одного терма, допускающего склейки с другим.
Причем склеивающиеся термы помечаются *.
Определение: Непомеченные термы называются первичными импликантами.
Полученное логическое выражение не всегда оказывается минимальным, поэтому исследуется возможность дальнейшего упрощения.
Для этого:
1. Составляются таблицы, в строках которых пишутся найденные первичные импликанты, а в столбцах указываются термы первичной ФАЛ.
2. Клетки этой таблицы отмечаются в том случае, если первичная импликанта входит в состав какого-нибудь первичного терма.
3. Задача упрощения сводится к нахождению такого минимального количества импликант, которые покрывают все столбцы.
Алгоритм метода Квайна (шаги):
1. Нахождение первичных импликант.
Исходные термы из ДНФ записывают в столбик и склеиваю сверху вниз.
Непомеченные импликанты переходят в функции на этом шаге.
2. Расстановка меток избыточности.
Составляем таблицу, в которой строки – первичные импликанты, столбцы – исходные термы. Если некоторый min-терм содержит первичный импликант, то на пересечении строки и столбца ставим метку.
3. Нахождение существенных импликант.
Если в каком-либо столбце есть только одна метка, то первичный импликант соответствующей строки является существенным.
4. Строка, содержащая существенный импликант и соответствующие столбцы вычеркиваются.
Если в результате вычеркивания столбцов появятся строки первичных импликант, которые не содержат метки или содержат одинаковые метки в строках, то такие первичные импликанты вычеркиваются. В последнем случае оставляем одну меньшего ранга.
5. Выбор минимального покрытия.
Из таблицы, полученной на шаге 3 выбирают такую совокупность первичных импликант, которая включает метки во всех столбцах по крайней мере по одной метке в каждом. При нескольких возможных вариантах отдается предпочтение покрытию с минимальным суммарным числом элементов в импликантах, образующих покрытие.
6. Далее результат записывается в виде функции.
|Термы 4го ранга |Термы 3го ранга |Термы 2го ранга |
|[pic] * 1 |[pic] |[pic] |
|[pic] * 3 |[pic] |[pic] |
Выбираем те min-термы, при записи которых, МДНФ функции минимальна.
Недостаток метода Квайна – необходимость полного по парного сравнения всех min-термов на этапе нахождения первичных импликант.
Идея модификации метода Квайна – метод Квайна-Мак-Класки. (1.4)
1. Каждая конъюнкция в ДСНФ представляется своим двоичным набором.
2. Вся совокупность номеров наборов разбивается на группы в зависимости от числа единиц, имеющихся в номерах наборов (0-группа, 1-группа, 2-группа и.т.д.).
3. Сравниваются две группы, отличающиеся на одну единицу.
4. В результате сравнения в номере набора, имеющего большее число единиц на позиции, где обнаружится разница на одну единицу ставится прочерк.
5. В процессе преобразования возникают новые сочетания (n-группы).
6. Процесс преобразования длится до тех пор, пока возможна операция склеивания.
7. Элементы преобразованных групп являются первичными импликантами, которые вместе с номерами исходных наборов образуют таблицы разметок.
8. В остальном эти методы совпадают с единственным уточнением – если в результате таблицы разметок ни одна из строк не покрывает единицу столбца, то надо выбрать номер столбца набора из предыдущей группы преобразований.
Определение: n-группа – это такой набор аргументов функции, что число всех аргументов равных единице равно n, причем значении функции равно 1.
Составим таблицу истинности:
|[pic] |[pic] |[pic] |[pic] |[pic] |
Синтез и минимизация логических функций
Краткая справка
Более подробный теоретический материал можно найти в [16,17,21,24]. Здесь и далее во всех формулах апостроф означает инверсию (отрицание).
Алгоритм "НИИРТА" графической минимизации булевых функций
Карта Карно на 8 переменных с прямоугольниками Карно.
Алгоритм проверки достоверности прямоугольника Карно(принцип симметрии)
Этот алгоритм необходимо применить дважды: относительно горизонтальных и относительно вертикальных осей симметрии.
Практикум по синтезу и минимизации логических функций
Приёмная комиссия в составе трех членов комиссии и одного председателя решает судьбу абитуриента большинством голосов. В случае равного распределения голосов большинство определяется той группой, в которой оказался председатель приемной комиссии. Построить автомат, обеспечивающий определение большинства голосов.
Пусть f - функция большинства голосов. f = 1, если большинство членов комиссии проголосовало за приём абитуриента, и f = 0 в противном случае.
Обозначим через x4 голос председателя комиссии. x4 = 1, если председатель комиссии проголосовал за приём абитуриента. x3, x2, x1 - голоса членов приёмной комиссии.
С учётом вышеуказанных допущений условие задачи можно однозначно представить в виде таблицы истинности.
Заполнение таблицы осуществляем с учётом того, что функция f является полностью определённой, т.е. она определена на всех возможных наборах переменных x1 - x4. Для n входных переменных существует N = 2n наборов переменных. В нашем Задачае N = 24 = 16 наборов.
Записывать эти наборы можно в любом порядке, но лучше в порядке возрастания двоичного кода.
Примечание. Здесь и далее под набором будем понимать конъюнкцию всех входных переменных. Существует множество научных определений для набора(конституента,терм,импликанта,минтерм и т.д.),но они только вносят путаницу.
Все наборы, на которых функция принимает значение 1. будем называть единичными, или рабочими. Наборы, на которых функция принимает значение 0, будем называть нулевыми, или запрещенными.
Для того, чтобы по таблице истинности найти функцию f, достаточно выписать все единичные наборы и соединить их знаком дизъюнкции.
Таким образом,
Полученная форма функции называется совершенной дизъюнктивной нормальной формой (СДНФ), так как каждое логическое слагаемое представляет собой конъюнкцию всех аргументов.
Очевидно, применяя основные законы булевой алгебры, мы могли бы аналитически уменьшить сложность полученного выражения. Но это наихудший способ минимизации булевых функций. Покажем это на предыдущем Задачае. Представим полученную функцию в виде логической суммы цифровых рабочих наборов:
Как мы потом увидим, результат минимизации должен быть компактнее. Но при аналитической минимизации придётся ввести неочевидную группировку: (1101+1111).
После длинных и неочевидных группировок удалось, наконец, получить правильное решение. При числе аргументов более 4-х аналитический метод минимизации не рационален.
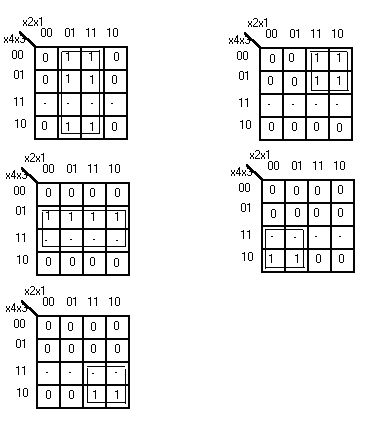
Применим карту Карно для решения задачи 1. На рисунке даны два варианта решения.
Эти выражения представляют собой Задача дизъюнктивной нормальной формы (ДНФ).
В некоторых случаях приведение результата минимизации к скобочной форме позволяет уменьшить количество ИС. необходимые для реализации булевой функции. Скобочная форма для f имеет вид:
Карта Карно для решения задачи 1.
Полностью определённая булева функция от 4-х переменных задана десятичными рабочими наборами. РН(4) = 5, 6, 7, 8, 9, 10, 11.Число в скобках указывает количество переменных. Найти минимальную форму этой функции.
Так как функция является полностью определённой, то запрещёнными наборами ЗН(4) являются наборы 0 - 4, 12 - 15. Исходя из этой информации, составляем таблицу истинности и осуществляем минимизацию по карте Карно.
По карте Карно получаем результат:
Решение задачи 2
Задание 1.1
Найти минимальную форму полностью определённых булевых функций, заданных 10-чными рабочим наборами :
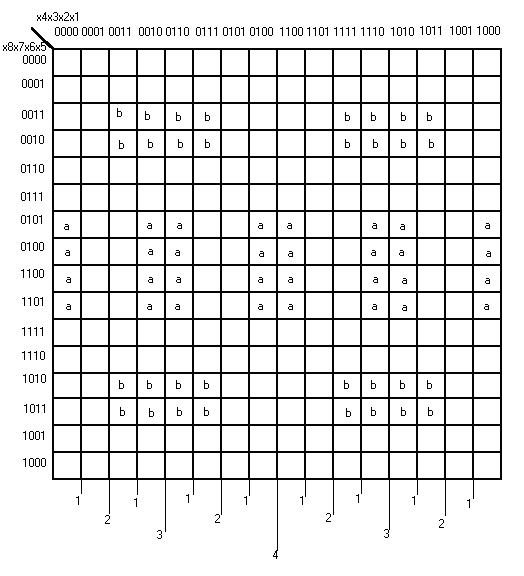
Найти минимальную форму функции y, представленной на рисунке.
Функция задана только на 5 наборах. Добавим к трём рабочим наборам ещё пять, а именно. 0000, 0011, 1000, 1011, 1010. Все оставшиеся наборы доопределим как запрещённые. В результате такого доопределения получим прямоугольник Карно, состоящий из 8 элементарных квадратов Карно. Этому прямоугольнику соответствует функция.
Решение задачи 3
Построить преобразователь двоичного кода, получаемого на выходе делителя частоты на 12, в двоично-десятичный код. Условие задачи отражено в таблице. Делитель работает в коде 8-4-2-1.
Для каждой функции yi заполняем карту Карно, производим доопределение и осуществляем минимизацию. Весь процесс отражён на рисунке.
В результате минимизации получаем систему функций:
Карты Карно к задаче 4.
Построить один разряд многоразрядного сумматора.
Пусть ai и вi - значения i-ых разрядов слагаемых а и в. Pi и Si - значения переноса и суммы на выходе i-го разряда, Pi-1 - значение переноса на выходе предыдущего разряда, тогда работу сумматора можно описать с помощью таблицы истинности.
Имеем систему полностью определённых булевых функций. Производим раздельную минимизацию (см. рисунок).
Решение задачи 5
Для реализации лучше Pi = aiвi + Pi-1(ai
вi)'. так как может быть использован общий для Si и Pi сомножитель (аi
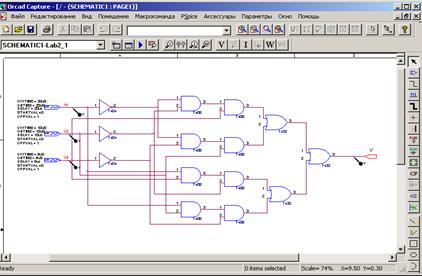
вi)'. Схема сумматора представлена на рисунке. Здесь же дано условное обозначение одноразрядного сумматора. где А и В - одноразрядные слагаемые, P0 и P1 - входной и выходной переносы, S1 - сумма.
На этом же рисунке изображён двухразрядный сумматор, выполненный на микросхеме 133ИМ2. Здесь А1, В1, А2, В2 - соответственно значения первых и вторых разрядов слагаемых А и В; S1 и S2 - 1-ый и 2-ой разряды суммы; P0 - входной перенос для первого разряда, P2' - выходной перенос.
Схемы сумматоров.
Задание 1.2