

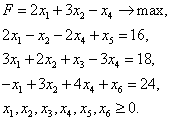

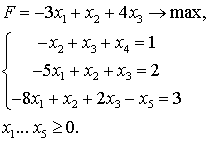
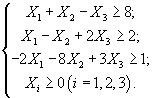





 Рейтинг: 4.2/5.0 (1842 проголосовавших)
Рейтинг: 4.2/5.0 (1842 проголосовавших)Категория: Windows: Математика
симплексным методом
Если вы уже разобрались с графическим методом решения задач линейного программирования. самое время переходить к симплекс-методу. В отличие от первого, он практически не имеет ограничений на задачу (любое количество переменных, разные знаки и т.п.) и модифицируется в зависимости от типа задачи (например, М-метод или метод искусственного базиса).
При решении задачи симплекс методом вычисления обычно ведутся (для компактности и наглядности) в таблицах (табличный симплекс-метод), причем последняя таблица с оптимальным решением содержит важную дополнительную информацию: решение двойственной задачи, остатки ресурсов, сведения о дефицитных ресурсах и т.п. которая позволяет провести экономический анализ задачи линейного программирования (см. ниже пример 3).
Примеры решений задач симплекс-методом выложены бесплатно для вашего удобства - изучайте, ищите похожие, решайте. Если вам нужна помощь в выполнении подобных заданий, перейдите в раздел: Решение задач линейного программирования .
Решение задач симплекс-методом: примеры онлайнЗадача 1. Компания производит полки для ванных комнат двух размеров - А и В. Агенты по продаже считают, что в неделю на рынке может быть реализовано до 550 полок. Для каждой полки типа А требуется 2 м2 материала, а для полки типа В - 3 м2 материала. Компания может получить до 1200 м2 материала в неделю. Для изготовления одной полки типа А требуется 12 мин машинного времени, а для изготовления одной полки типа В - 30 мин; машину можно использовать 160 час в неделю. Если прибыль от продажи полок типа А составляет 3 денежных единицы, а от полок типа В - 4 ден. ед. то сколько полок каждого типа следует выпускать в неделю?
Задача 2. Решить задачу линейного программирования симплекс-методом. 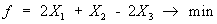
Задача 3. Предприятие производит 3 вида продукции: А1, А2, А3, используя сырьё двух типов. Известны затраты сырья каждого типа на единицу продукции, запасы сырья на планируемый период, а также прибыль от единицы продукции каждого вида.
Для производства двух видов изделий А и В используются три типа технологического оборудования. Для производства единицы изделия А оборудование первого типа используется в течении 1 часа, оборудование второго типа – 3 часа, оборудование третьего типа – 3 часа.
Для производства единицы изделия В оборудование первого типа используется в течении 2 часа, оборудование второго типа – 3 часа, оборудование третьего типа – 1 час.
На изготовление всех изделий предприятие может использовать оборудование первого типа не более чем 32 часа, оборудование второго типа – 60 часов, оборудование третьего типа – 50 часов.
Прибыль от реализации единицы готового изделия А составляет 4 денежные единицы, а изделия В – 2 денежные единицы.
Составить план производства изделий А и В, обеспечивающий максимальную прибыль от их реализации.
1) Составить математическую модель задачи
2) Решить графическим методом
3)Решить симплекс-методом путем преобразования симплекс-таблиц
Перед нами – классическая задача линейного программирования. Под планом производства понимается ответ на простой вопрос: сколько изделий А и сколько изделий В надо выпустить, чтобы прибыль была максимальна.
Прибыль рассчитывается по формуле:  .
.
Запишем математическую модель задачи:
Чтобы проиллюстрировать применение симплекс-метода решения этой задачи, решим ее графически.
Для этого построим на плоскости  области, описываемые ограничениями-неравенствами, и прямую
области, описываемые ограничениями-неравенствами, и прямую  , которая называется целевой функцией.
, которая называется целевой функцией.
Три записанных выше неравенства ограничивают на плоскости многоугольник (построен красным цветом), ограниченный слева и снизу координатными осями (т.к. искомое количество изделий положительно).
График целевой функции (построен синим цветом) передвигается в направлении, обозначенном стрелкой (по-научному – в направлении своего градиента), до тех пор, пока не достигнет граничной точки многоугольника – в нашем случае это точка – (15 ; 5). В этой точке целевая функция будет достигать максимума.
А теперь решим эту задачу симплекс-методом. Для этого перейдем от ограничений-неравенств к ограничениям-равенствам, введя дополнительные переменные  .
.
Симплекс-таблица составляется так:
В графе Базис записываются вектора переменных, принимаемые за базисные. На первом этапе это – A3, A4, A5. Базисными будут переменные, каждая из которых входит только в одно уравнение системы, и нет такого уравнения, в которое не входила бы хотя бы одна из базисных переменных.
В следующий столбец  записываются коэффициенты целевой функции, соответствующие каждой переменной. Столбец В – столбец свободных членов. Далее идут столбцы коэффициентов Аi при i –й переменной.
записываются коэффициенты целевой функции, соответствующие каждой переменной. Столбец В – столбец свободных членов. Далее идут столбцы коэффициентов Аi при i –й переменной.
Под столбцом свободных членов записывается начальная оценка 
Остальные оценки записываются под столбцами соответствующих векторов  .
.
Следует отметить, что оценки для базисных векторов всегда равны нулю.
Преобразование симплекс-таблицы ведется следующим образом:
Шаг 1: Проверяется критерий оптимальности, суть которого состоит в том, что все оценки  должны быть неотрицательны. В нашем случае этот критерий не выполнен, поэтому переходим ко второму шагу.
должны быть неотрицательны. В нашем случае этот критерий не выполнен, поэтому переходим ко второму шагу.
Шаг 2: Для отрицательных оценок вычисляются величины:
Из этих элементов выбирается тот, для которого вычисленное произведение минимально, в нашем случае  минимально, поэтому в качестве так называемого разрешающего элемента выбирается третий элемент первого столбца – 3 (выделен в таблице).
минимально, поэтому в качестве так называемого разрешающего элемента выбирается третий элемент первого столбца – 3 (выделен в таблице).
Шаг 3: Третья строка таблицы делится на 3 и вычитается из первой и второй строк. В сущности, применяется метод исключения неизвестных, известный как метод Жордана – Гаусса.
Таким образом, новыми базисными переменными становятся A3, A4, A1.
Возвращаемся к шагу 1 и повторяем весь процесс.
Под столбцом свободных членов записывается начальная оценка 
Остальные оценки записываются под столбцами соответствующих векторов  .
.
Следует отметить, что оценки для базисных векторов всегда равны нулю.
Опять проверяется критерий оптимальности. Отрицательная оценка только одна – в столбце А2.
Вычисляем:
Разрешающим элементом будет второй элемент второго столбца – 2/3.
Новыми базисными переменными становятся A3, A2, A1
Делим вторую строку на 2 и вычитаем из третьей.
Умножаем вторую строку на 5/2 и вычитаем из первой.
Рассмотрен пример решения задачи, в которой начальный базис находится симплекс М методом.
Условие задачиНайти оптимальные величины производства продукции видов А, Б и В. Затраты сырья на единицу продукции: А – 5, Б – 2, В – 4. Объем сырья – 2000 единиц. Затраты оборудования на единицу продукции: А – 4, Б – 5, В – 4. Объем оборудования – 1000 единиц. Прибыль от реализации единицы продукции: А – 10, Б – 8, В – 12. Критерий – максимум прибыли предприятия. Производство продукции А должно быть не менее 100 ед. Производство продукции Б должно быть не менее 50 ед.
Решение задачи симплекс методом1) Определение оптимального плана производства
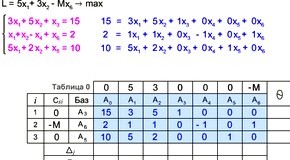
Пусть x1 . x2 . x3 - количество произведенной продукции вида А, Б, В, соответственно. Тогда математическая модель задачи имеет вид:
 =100>
=100>
Решаем симплекс методом.
Вводим дополнительные переменные x4 ≥ 0, x5 ≥ 0, x6 ≥ 0, x7 ≥ 0, чтобы неравенства преобразовать в равенства.
Чтобы выбрать начальный базис, вводим искусственные переменные x8 ≥ 0, x9 ≥ 0 и очень большое число M (M –> ∞). Решаем М методом.
Данные заносим в симплекс таблицу
Симплекс таблица № 1Целевая функция:
 0 · 2000 + 0 · 1000 + (– M) · 100 + (– M) · 50 = – 150M
0 · 2000 + 0 · 1000 + (– M) · 100 + (– M) · 50 = – 150M
Вычисляем оценки по формуле:
Δ1 = 0 · 5 + 0 · 4 + (– M) · 1 + (– M) · 0 – 10 = – M – 10
Δ2 = 0 · 2 + 0 · 5 + (– M) · 0 + (– M) · 1 – 8 = – M – 8
Δ3 = 0 · 4 + 0 · 4 + (– M) · 0 + (– M) · 0 – 12 = – 12
Δ4 = 0 · 1 + 0 · 0 + (– M) · 0 + (– M) · 0 – 0 = 0
Δ5 = 0 · 0 + 0 · 1 + (– M) · 0 + (– M) · 0 – 0 = 0
Δ6 = 0 · 0 + 0 · 0 + (– M) · (–1) + (– M) · 0 – 0 = M
Δ7 = 0 · 0 + 0 · 0 + (– M) · 0 + (– M) · (–1) – 0 = M
Δ8 = 0 · 0 + 0 · 0 + (– M) · 1 + (– M) · 0 – (– M) = 0
Δ9 = 0 · 0 + 0 · 0 + (– M) · 0 + (– M) · 1 – (– M) = 0
Поскольку есть отрицательные оценки, то план не оптимален. Наименьшая оценка:
Δ1 = – M – 10
Вводим переменную x1 в базис.
Определяем переменную, выходящую из базиса. Для этого находим наименьшее неотрицательное отношение  для столбца x1 .
для столбца x1 .
Наименьшее неотрицательное: Q3 = 100. Выводим переменную x8 из базиса. Для этого над строками таблицы выполняем линейные преобразования.
Из 1-й строки вычитаем 3-ю строку, умноженную на 5
Из 2-й строки вычитаем 3-ю строку, умноженную на 4
Получаем новую таблицу:
Симплекс таблица № 2Целевая функция:
 0 · 1500 + 0 · 600 + 10 · 100 + (– M) · 50 = – 50M + 1000
0 · 1500 + 0 · 600 + 10 · 100 + (– M) · 50 = – 50M + 1000
Вычисляем оценки по формуле:
Δ1 = 0 · 0 + 0 · 0 + 10 · 1 + (– M) · 0 – 10 = 0
Δ2 = 0 · 2 + 0 · 5 + 10 · 0 + (– M) · 1 – 8 = – M – 8
Δ3 = 0 · 4 + 0 · 4 + 10 · 0 + (– M) · 0 – 12 = – 12
Δ4 = 0 · 1 + 0 · 0 + 10 · 0 + (– M) · 0 – 0 = 0
Δ5 = 0 · 0 + 0 · 1 + 10 · 0 + (– M) · 0 – 0 = 0
Δ6 = 0 · 5 + 0 · 4 + 10 · (–1) + (– M) · 0 – 0 = – 10
Δ7 = 0 · 0 + 0 · 0 + 10 · 0 + (– M) · (–1) – 0 = M
Δ8 = 0 · (–5) + 0 · (–4) + 10 · 1 + (– M) · 0 – (– M) = M + 10
Δ9 = 0 · 0 + 0 · 0 + 10 · 0 + (– M) · 1 – (– M) = 0
Поскольку есть отрицательные оценки, то план не оптимален. Наименьшая оценка:
Δ2 = – M – 8
Вводим переменную x2 в базис.
Определяем переменную, выходящую из базиса. Для этого находим наименьшее неотрицательное отношение  для столбца x2 .
для столбца x2 .
Наименьшее неотрицательное: Q4 = 50. Выводим переменную x9 из базиса и удаляем искусственные переменные. Выполняем линейные преобразования.
Из 1-й строки вычитаем 4-ю строку, умноженную на 2
Из 2-й строки вычитаем 4-ю строку, умноженную на 5
Получаем новую таблицу:
Симплекс таблица № 3Целевая функция:
 0 · 1400 + 0 · 350 + 10 · 100 + 8 · 50 = 1400
0 · 1400 + 0 · 350 + 10 · 100 + 8 · 50 = 1400
Вычисляем оценки по формуле:
Δ1 = 0 · 0 + 0 · 0 + 10 · 1 + 8 · 0 – 10 = 0
Δ2 = 0 · 0 + 0 · 0 + 10 · 0 + 8 · 1 – 8 = 0
Δ3 = 0 · 4 + 0 · 4 + 10 · 0 + 8 · 0 – 12 = – 12
Δ4 = 0 · 1 + 0 · 0 + 10 · 0 + 8 · 0 – 0 = 0
Δ5 = 0 · 0 + 0 · 1 + 10 · 0 + 8 · 0 – 0 = 0
Δ6 = 0 · 5 + 0 · 4 + 10 · (–1) + 8 · 0 – 0 = – 10
Δ7 = 0 · 2 + 0 · 5 + 10 · 0 + 8 · (–1) – 0 = – 8
Поскольку есть отрицательные оценки, то план не оптимален. Наименьшая оценка:
Вводим переменную x3 в базис.
Определяем переменную, выходящую из базиса. Для этого находим наименьшее неотрицательное отношение  для столбца x3 .
для столбца x3 .
2-ю строку делим на 4.
Из 1-й строки вычитаем 2-ю строку, умноженную на 4
Получаем новую таблицу:
Симплекс таблица № 4Целевая функция:
 0 · 1050 + 12 · 175/2 + 10 · 100 + 8 · 50 = 2450
0 · 1050 + 12 · 175/2 + 10 · 100 + 8 · 50 = 2450
Вычисляем оценки по формуле:
Δ1 = 0 · 0 + 12 · 0 + 10 · 1 + 8 · 0 – 10 = 0
Δ2 = 0 · 0 + 12 · 0 + 10 · 0 + 8 · 1 – 8 = 0
Δ3 = 0 · 0 + 12 · 1 + 10 · 0 + 8 · 0 – 12 = 0
Δ4 = 0 · 1 + 12 · 0 + 10 · 0 + 8 · 0 – 0 = 0
Δ5 = 0 · (–1) + 12 · 1/4 + 10 · 0 + 8 · 0 – 0 = 3
Δ6 = 0 · 1 + 12 · 1 + 10 · (–1) + 8 · 0 – 0 = 2
Δ7 = 0 · (–3) + 12 · 5/4 + 10 · 0 + 8 · (–1) – 0 = 7
Поскольку отрицательных оценок нет, то план оптимален.
То есть необходимо произвести x1 = 100 единиц продукции вида А, x2 = 50 единиц продукции вида Б и x3 = 87,5 единиц продукции вида В. Максимальная прибыль при этом составит Fmax = 2450 единиц.
 Один из методов решения оптимизационных задач (как правило связанных с нахождением минимума или максимума ) линейного программирования называется симплекс-методом. Симплекс-метод включает в себя целую группу алгоритмов и способов решения задач линейного программирования. Один из таких способов, предусматривающий запись исходных данных и их пересчет в специальной таблице, носит наименование табличного симплекс-метода .
Один из методов решения оптимизационных задач (как правило связанных с нахождением минимума или максимума ) линейного программирования называется симплекс-методом. Симплекс-метод включает в себя целую группу алгоритмов и способов решения задач линейного программирования. Один из таких способов, предусматривающий запись исходных данных и их пересчет в специальной таблице, носит наименование табличного симплекс-метода .
Рассмотрим алгоритм табличного симплекс-метода на примере решения производственной задачи. которая сводится к нахождению производственного плана обеспечивающего максимальную прибыль.
Исходные данные задачи на симплекс-методФонд времени работы станков (мин.) задан в матрице B:
Прибыль от продажи каждой единицы изделия (руб./шт.) задана матрицей C:
Цель производственной задачи Решение задачи табличным симплекс-методом(1) Обозначим X1, X2, X3, X4 планируемое количество изделий каждого вида. Тогда искомый план: (X1, X2, X3, X4 )
(2) Запишем ограничения плана в виде системы уравнений:
(3) Тогда целевая прибыль:
То есть прибыль от выполнения производственного плана должна быть максимальной.
(4) Для решения получившейся задачи на условный экстремум, заменим систему неравенств системой линейных уравнений путем ввода в нее дополнительных неотрицательных переменных (X5, X6, X7 ).
(5) Примем следующий опорный план :
X1 = 0, X2 = 0, X3 = 0, X4 = 0, X5 = 252, X6 = 144, X7 = 80
(6) Занесем данные в симплекс-таблицу :
. В последнюю строку заносим коэффициенты при целевой функции и само ее значение с обратным знаком;
(7) Выбираем в последней строке наибольшее (по модулю ) отрицательное число.
Вычислим b = Н / Элементы_выбранного_столбца
Среди вычисленных значений b выбираем наименьшее .
Пересечение выбранных столбца и строки даст нам разрешающий элемент. Меняем базис на переменную соответствующую разрешающему элементу (X5 на X1 ).
(8) Теперь необходимо пересчитать все элементы симплекс-таблицы, кроме столбца b. Вот как это можно сделать:
Как видите, мы берем текущую пересчитываемую ячейку и ячейку с разрешающим элементом. Они образуют противоположные углы прямоугольника. Далее перемножаем значения из ячеек 2-х других углов этого прямоугольника. Это произведение (A * B ) делим на разрешающий элемент (РЭ ). И вычитаем из текущей пересчитываемой ячейки (aij ) то, что получилось. Получаем новое значение - aij (*) .
(9) Вновь проверяем последнюю строку (c ) на наличие отрицательных чисел. Если их нет – оптимальный план найден, переходим к последнему этапу решения задачи. Если есть – план еще не оптимален, и симплекс-таблицу вновь нужно пересчитать.
Так как у нас в последней строке снова имеются отрицательные числа, начинаем новую итерацию вычислений.
(10) Так как в последней строке нет отрицательных элементов, это означает, что нами найден оптимальный план производства! А именно: выпускать мы будем те изделия, которые перешли в колонку «Базис» - X1 и X2. Прибыль от производства каждой единицы продукции нам известна (матрица C ). Осталось перемножить найденные объемы выпуска изделий 1 и 2 с прибылью на 1 шт. получим итоговую (максимальную! ) прибыль при данном плане производства.
X1 = 32 шт. X2 = 20 шт. X3 = 0 шт. X4 = 0 шт.
P = 48 * 32 + 33 * 20 = 2 196 руб.
Галяутдинов Р.Р.
Производя расчеты по симплекс-методу, нет необходимости выписывать все вычисления столь подробно, как мы делали это в предыдущих примерах. Оказывается, весь процесс можно записать в виде последовательности однотипно заполняемых таблиц, причем каждому шагу будет отвечать переход к следующей таблице.
Описание симплекс-таблиц произведем на примере задачи (8.4), (8.5), где требуется минимизировать функцию (8.5) при ограничениях (8.4) и условиях Xj > 0 (/ = I. 5).
Для заполнения первой таблицы необходимо в каждом из уравнений (8.4) перенести все члены, кроме свободного, из правой части в левую, т. е. записать (8.4) в виде :
■ х2 -р44-ру5 = р, (8.20)
х3-у4х4-у5х5 = У-Аналогичную работу следует проделать и с равенством (8.5):
/54х4 55х5 = 8.
Заглавная строка таблицы и характер заполнения, не считая стрелок, в комментариях не нуждаются. Расстановку стрелок поясним ниже.
В соответствии с ранее описанной методикой мы должны прежде всего выяснить, имеется ли в первоначальном выражении для
/= 54х4 + б5х5 + 5
хотя бы один отрицательный коэффициент при х4 и х5. Поскольку при внесении в таблицу коэффициенты при х4 и х5 поменяли знаки,
то мы должны, следовательно, выяснить, имеются ли в последней строке таблицы (не считая свободного члена 6) положительные числа. Если таковых нет, то базисное решение, отвечающее данному базису, т. е. (а, р, у, 0,0), является оптимальным, a min/ = 8— задача решена.
Предположим, что в последней строке имеется (не считая 8) положительное число 84. Отмечаем столбец, в котором оно находится,
вертикальной стрелкой. Далее просматриваем остальные числа этого столбца. Если среди них нет отрицательных чисел — это означает, что а4 > 0, р4 > 0, у4 £ 0, и мы имеем случай II. Тогда min/= со, и процесс снова прекращается.
Пусть, наконец, среди чисел отмеченного столбца, кроме последнего числа, имеются положительные числа. Это означает, что мы
имеем случай III и, следовательно, должны сделать шаг. Например, как мы считали ранее, пусть -а4>0, -Р4>0 (это означает а4<0, Р4 < 0), a -у4 > 0 (т. е. у4 < 0), в точном соответствии с предположением (8.7) § 8.1. В этом случае описанная ранее методика предписывает составить отношения
и выбрать из них наименьшее.
п а Пусть, например, таковым является отношение отвечающее строке таблицы с базисным неизвестным хх. Отмечаем эту строку горизонтальной стрелкой. Элемент таблицы, стоящий в отмеченном столбце и отмеченной строке, называется разрешаю-* щим элементом. В данном случае это -а4 (в таблице он обведен пунктиром).
С этого момента начинается перестройка таблицы, цель которой состоит в переходе к новому базису <х4, х2, Ху). Ее можно осуществить при помощи все того же метода Гаусса. А именно умножаем выделенную строку на такое число, чтобы на месте разрешающего
— „. _„ на ^ Это с_
вуеттому, что первое из уравнений (8.20) разрешается относительно нового базисного неизвестного х4. Полученную таким образом новую строку вписываем уже в новую таблицу снова в виде первой строки. Затем к каждой из остальных строк таблицы 1 прибавляем вновь полученную строку, умноженную на такое число, чтобы в клетке отмеченного столбца появился нуль — это соответствует исключению неизвестного х4 из остальных уравнений, а также из
выражения для /. Преобразованные таким образом строки пишем в новую таблицу на место прежних строк. В результате получаем новую таблицу 2.
К новой таблице применяется та же процедура. В результате или находится оптимальное решение (случай I), или обнаруживается, что min/= со (случай II), или же производится следующий шаг (случай III) — получаем новую таблицу 3. И так далее, пока процесс не остановится (случай I или случай III).
Вот как будет выглядеть при такой методике решение примера 1 § 8.1. Исходная таблица имеет вид:
На данной странице установлена программа на языке Java (апплет), которая решает on-line (онлайн) задачу линейного программирования (ЛП) бесплатно. Для решения задачи ЛП применен симплекс-метод. Для работы апплета реализующего симплекс-метод на вашем компьютере должна быть установлена Java, ссылка для установки http://www.java.com/ru/download/
Для разрешения выполнения апплета на вашем компьютере надо сделать следующее - нажать кнопку Пуск>Панельуправления>Программы>Java. В окне Java Control Panel выбираем вкладку Security (Безопастность) нажимаем кнопку Edit Site List, кнопку add и вставляем в свободное поле путь к этой страницы из адресной строки браузера. Далее нажимаем кнопки ОК, после этого перезагружаем компьютер.
Для запуска апплета нажмите на кнопку "Simplex". Если над этой строкой не видна кнопка "Simplex", то на компьютере не установлена Java.
После нажатия на кнопку « Simplex » выводится первое окно для ввода числа переменных и числа ограничений задачи на симплекс-метод.
После нажатия на кнопку « ok » выводится окно для ввода остальных данных задачи на симплекс-метод: режима отображения (десятичные дроби или обыкновенные), тип критерия задачи min или max. ввод коэффициентов целевой функции и коэффициентов системы ограничений со знаками « ≤ », « ≥ » или « = », ограничения вида хi ≥ 0 вводить не надо, симплекс-метод их учитывает в своем алгоритме.
После нажатия на кнопку «Решить» выводится окно с результатами решения задачи на симплекс-метод. Окно состоит из двух частей, в верхней части находится текстовое поле, содержащее описание приведения исходной задачи к канонической форме, которая используется для составления первой симплекс-таблицы. В нижней части окна в панели со вкладками расположены симплекс-таблицы каждой итерации с небольшим текстовым полем внизу с указанием разрешающего столбца, разрешающей строки и другой информации, что делает программу обучающей. Во вкладке с оптимальной (последней) таблицей в текстовом поле приведено полученное оптимальное решение задачи.
Замеченные ошибки и комментарии по работе апплета присылайте на mathelp6@gmail.com или звоните  8 962 700 77 06, за что мы будем Вам очень благодарны.
8 962 700 77 06, за что мы будем Вам очень благодарны.
Программа М-метод скачать
Программа для решения транспортной задачи скачать
Здесь приведено ручное (не апплетом) решение двух задач симплекс-методом (аналогичным решению апплетом) с подробными объяснениями для того, чтобы понять алгоритм решения задач. Первая задача содержит знаки неравенства только " ≤ " (задача с начальным базисом), вторая может содержить знаки " ≥ ", " ≤ " или " = " (задача с искусственным базисом), они решаются по разному.
Симплекс-метод, решение задачи с начальным базисом1)Симплекс-метод для задачи с начальным базисом (все знаки неравенств-ограничений " ≤ ").
Запишем задачу в канонической форме, т.е. ограничения-неравенства перепишем в виде равенств, добавляя балансовые переменные:
Эта система является системой с базисом (базис s1. s2. s3. каждая из них входит только в одно уравнение системы с коэффициентом 1), x1 и x2 - свободные переменные. Задачи, при решении которых применяется симплекс-метод, должны обладать следующими двумя свойствами:
-система ограничений должна быть системой уравнений с базисом;
-свободные члены всех уравнений в системе должны быть неотрицательны.
Полученная система - система с базисом и ее свободные члены неотрицательны, поэтому можно применить симплекс-метод. Составим первую симплекс-таблицу (Итерация 0), т.е. таблицу коэффициентов целевой функции и системы уравнений при соответствующих переменных. Здесь "БП" означает столбец базисных переменных, «Решение» - столбец правых частей уравнений системы. Решение не является оптимальным, т.к. в z – строке есть отрицательные коэффициенты.
Если вам понадобится решить задачу линейного программирования с помощью симплекс-таблиц, то наш онлайн сервис вам окажет большую помощь. Симплекс-метод подразумевает последовательный перебор всех вершин области допустимых значений с целью нахождения той вершины, где функция принимает экстремальное значение. На первом этапе находится какое-нибудь решение, которое улучшается на каждом последующем шаге. Такое решение называется базисным. Приведем последовательность действий при решении задачи линейного программирования симплекс-методом:
Первый шаг. В составленной таблице перво-наперво необходимо просмотреть столбец со свободными членами. Если в нем имеются отрицательные элементы, то необходимо осуществить переход ко второму шагу, есле же нет, то к пятому.
Второй шаг. На втором шаге необходимо определиться, какую переменную изключить из базиса, а какую включить, для того, что бы произвести перерасчет симплекс-таблицы. Для этого просматриваем столбец со свободными членами и находим в нем отрицательный элемент. Строка с отрицательным элементом будет называться ведущей. В ней находим максимальный по модулю отрицательный элемент, соответсвующий ему столбец - ведомый. Если же среди свободных членов есть отрицательные значения, а в соответсвующей строке нет, то такая таблица не будет иметь решений. Переменая в ведущей строке, находящаяся в столбце свободных членов исключается из базиса, а переменная соответсвующая ведущему столцу включается в базис.
Для скачивания работы включите JavaScript в Вашем браузере
Решение х0 называется оптимальным, если для него выполняется условие сТ х0 сТ х. для всех х Rx. Поскольку min fx эквивалентен max - fx. то задачу линейного программирования всегда можно свести к эквивалентной задаче максимизации. Для решения задач данного типа применяются методы 1 графический 2 табличный прямой, простой симплекс - метод 3 метод искусственного базиса 4 модифицированный симплекс - метод 5 двойственный симплекс - метод. 1.2 Табличный симплекс - метод
Для его применения необходимо, чтобы знаки в ограничениях были вида меньше либо равно. а компоненты вектора b - положительны. Алгоритм решения сводится к следующему Приведение системы ограничений к каноническому виду путм введения дополнительных переменных для приведения неравенств к равенствам. Если в исходной системе ограничений присутствовали знаки равно или больше либо равно. то в указанные ограничения добавляются искусственные переменные, которые так же вводятся и в
целевую функцию со знаками, определяемыми типом оптимума. Формируется симплекс-таблица. Рассчитываются симплекс-разности. Принимается решение об окончании либо продолжении счта. При необходимости выполняются итерации. На каждой итерации определяется вектор, вводимый в базис, и вектор, выводимый из базиса. Таблица пересчитывается по методу
Жордана-Гаусса или каким-нибудь другим способом. 1.3 Метод искусственного базиса Данный метод решения применяется при наличии в ограничении знаков равно. больше либо равно. меньше либо равно и является модификацией табличного метода. Решение системы производится путм ввода искусственных переменных со знаком, зависящим от типа оптимума, т.е. для исключения из базиса этих переменных последние вводятся в целевую функцию с большими отрицательными
Продолжение на след. странице