



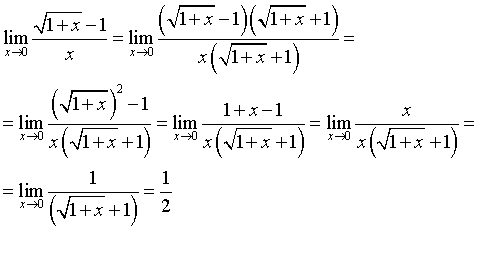




 Рейтинг: 4.9/5.0 (1912 проголосовавших)
Рейтинг: 4.9/5.0 (1912 проголосовавших)Категория: Windows: Документы
Первым замечательным пределом именуют следующее равенство:
Так как при $\alpha \to 0$ имеем $\sin \alpha \to 0$, то говорят, что первый замечательный предел раскрывает неопределённость вида $\frac <0> <0>$. Вообще говоря, в формуле (1) вместо переменной $\alpha$ под знаком синуса и в знаменателе может быть расположено любое выражение, – лишь бы выполнялись два условия:
Часто используются также следствия из первого замечательного предела:
На данной странице решены одиннадцать примеров. Пример №1 посвящен доказательству формул (2)-(4). Примеры №2, №3, №4 и №5 содержат решения с подробными комментариями. Примеры №6-10 содержат решения практически без комментариев, ибо подробные пояснения были даны в предыдущих примерах. При решении используются некоторые тригонометрические формулы, которые можно найти тут .
Замечу, что наличие тригонометрических функций вкупе с неопределённостью $\frac <0> <0>$ ещё не означает обязательное применение первого замечательного предела. Иногда бывает достаточно простых тригонометрических преобразований, – например, см. пример №11.
а) Так как $\mathrm
Так как $\cos 0=1$ и $ \lim_<\alpha \to 0> \frac <\sin \alpha ><\alpha>=1$, то $\lim_<\alpha \to 0> \frac <\sin \alpha><\alpha> \cdot \lim_<\alpha \to 0> \frac<1><\cos \alpha>=1\cdot 1=1$. Равенство доказано.
б) Сделаем замену $\alpha=\sin y$. Поскольку $\sin0=0$, то условия $\alpha \to 0$ и $y \to 0$ эквивалентны. Кроме того, в окрестности нуля $ \arcsin\alpha=\arcsin(\sin y)=y$, поэтому:
в) Сделаем замену $\alpha=\mathrm
Равенство $ \lim_<\alpha \to 0> \frac <\mathrm
Равенства а), б), в) часто используются наряду с первым замечательным пределом.
Так как $\lim_
Итак, оба условия, перечисленные в начале страницы, выполнены. Из этого следует, что применима формула (1). т.е. $\lim_
Так как $ \lim_
Теперь выражения в знаменателе и под знаком синуса совпали. Оба условия для предела $\lim_
Так как $\lim_
Так как $\lim_
Инструкция
В математическом анализе существуют понятия пределов последовательностей и функций. Когда требуется найти предел последовательности, это записывают следующим образом: lim xn=a. В такой последовательности последовательности xn стремится к a, а n к бесконечности. Последовательность обычно представляют в виде ряда, например:
Данный предел равен нулю, поскольку n>?, а последовательность 1/n^2 стремится к нулю.
Обычно переменная величина x стремится к конечному пределу a, причем, x постоянно приближается к a, а величина a постоянна. Это записывают следующим образом: limx =a, при этом, n также может стремиться как к нулю, так и к бесконечности. Существуют бесконечные функции, для них предел стремится к бесконечности. В других случаях, когда, например, функцией описывается замедление хода поезда, можно говорить о пределе, стремящемся к нулю.
У пределов имеется ряд свойств. Как правило, любая функция имеет только один предел. Это главное свойство предела. Другие их свойства перечислены ниже:
* Предел суммы равен сумме пределов:
lim(x+y)=lim x+lim y
* Предел произведения равен произведению пределов:
lim(xy)=lim x*lim y
* Предел частного равен частному от пределов:
lim(x/y)=lim x/lim y
* Постоянный множитель выносят за знак предела:
lim(Cx)=C lim x
Если дана функция 1 /x, в которой x >?, ее предел равен нулю. Если же x>0, предел такой функции равен ?.
Для тригонометрических функций имеются исключения из этих правил. Так как функция sin x всегда стремится к единице, когда приближается к нулю, для нее справедливо тождество:
В ряде задач встречаются функции, при вычислении пределов которых возникает неопределенность - ситуация, при которой предел невозможно вычислить. Единственным выходом из такой ситуации становится применение правила Лопиталя. Существует два вида неопределенностей:
* неопределенность вида 0/0
* неопределенность вида ?/?
К примеру, дан предел следующего вида: lim f(x)/l(x), причем, f(x0)=l(x0)=0. В таком случае, возникает неопределенность вида 0/0. Для решения такой задачи обе функции подвергают дифференцированию, после чего находят предел результата. Для неопределенностей вида 0/0 предел равен:
lim f(x)/l(x)=lim f'(x)/l'(x) (при x>0)
Это же правило справедливо и для неопределенностей типа ?/?. Но в этом случае справедливо следующее равенство: f(x)=l(x)=?
С помощью правила Лопиталя можно находить значения любых пределов, в которых фигурируют неопределенности. Обязательное условие при
том - отсутствие ошибок при нахождении производных. Так, например, производная функции (x^2)' равна 2x. Отсюда можно сделать вывод, что:
Пример 1. Найти предел функции
Lim((x^2-3*x)/(2*x+5),x=3).
Решение: Такого сорта примеры по теории вычисляют обычной подстановкой
Предел равен 18/11.
Ничего сложного и мудрого в таких пределах нет - подставили значение, вычислили, записали предел в ответ. Однако на базе таких пределов всех приучают, что прежде всего нужно подставить значение в функцию. Далее пределы усложняют, вводят понятие бесконечности, неопределенности и тому подобные.
Предел с неопределенностью типа бесконечность разделить на бесконечность. Методы раскрытия неопределенностиПример 2. Найти предел функции
Lim((x^2+2x)/(4x^2+3x-4),x=infinity).
Решение: Задан предел вида полином разделить на полином, причем переменная стремится к бесконечности
Простая подстановка значения к которому следует переменная найти пределов не поможет, получаем неопределенность вида бесконечность разделить на бесконечность.
Пот теории пределов алгоритм вычисления предела заключается в нахождении наибольшего степени "икс" в числителе или знаменателе. Далее на него упрощают числитель и знаменатель и находят предел функции
Поскольку значение 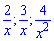 стремятся к нулю при переменной к бесконечности то ими пренебрегают, или записывают в конечный выражение в виде нулей
стремятся к нулю при переменной к бесконечности то ими пренебрегают, или записывают в конечный выражение в виде нулей
Сразу из практики можно получить два вывода которые являются подсказкой в вычислениях. Если переменная стремится к бесконечности и степень числителя больше от степени знаменателя то предел равен бесконечности. В противном случае, если полином в знаменателе старшего порядка чем в числителе предел равен нулю.
Формулами предел можно записать так
Если имеем функцию вида обычный поленом без дробей то ее предел равен бесконечности
Следующий тип пределов касается поведения функций возле нуля.
Пример 3. Найти предел функции
Lim((x^2+3x-5)/(x^2+x+2), x=0).
Решение: Здесь уже выносить старший множитель полинома не требуется. С точностью до наоборот, необходимо найти наименьший степень числителя и знаменателя и вычислить предел
Значение x^2; x стремятся к нулю когда переменная стремится к нулю  Поэтому ими пренебрегают, таким образом получим
Поэтому ими пренебрегают, таким образом получим
что предел равен 2,5.
Теперь Вы знаете как найти предел функции вида полином разделить на полином если переменная стремится к бесконечности или 0. Но это лишь небольшая и легкая часть примеров. Из следующего материала Вы научитесь как раскрывать неопределенности пределов функции .
Предел с неопределенностью типа 0/0 и методы его вычисленийСразу все вспоминают правило согласно которому делить на ноль нельзя. Однако теория пределов в этом контексте подразумеваем бесконечно малые функции.
Рассмотрим для наглядности несколько примеров.
Пример 4. Найти предел функции
Lim((3x^2+10x+7)/(x+1), x=-1).
Решение: При подстановке в знаменатель значения переменной x = -1 получим ноль, то же самое получим в числителе. Итак имеем неопределенность вида 0/0.
Бороться с такой неопределенностью просто: нужно разложить полином на множители, а точнее выделить множитель, который превращает функцию в ноль.
После разложения предел функции можно записать в виде
Вот и вся методика вычисления предела функции. Так же поступаем если есть предел вида многочлен разделить на многочлен.
Пример 5. Найти предел функции
Lim((2x^2-7x+6)/(3x^2-x-10), x=2).
Решение: Прямая подстановка показывает
2*4-7*2+6=0;
3*4-2-10=0
что имеем неопределенность типа 0/0.
Разделим полиномы на множитель которій вносит особенность
Есть преподаватели которые учат, что полиномы 2 порядка то есть вида "квадратные уравнения" следует решать через дискриминант. Но реальная практика показывает что это дольше и запутаннее, поэтому избавляйтесь особенности в пределах по указанному алгоритму. Таким образом записываем функцию в виде простых множителей и вічисляем в предел
Как видите, ничего сложного в исчислении таких пределов нет. Делить многочлены Вы на момент изучения пределов умеете, по крайней мере согласно программе должны уже пройти.
Среди задач на неопределенность типа 0/0 встречаются такие в которых нужно применять формулы сокращенного умножения. Но если Вы их не знаете, то делением многочлена на одночлен можно получить нужную формулу.
Пример 6. Найти предел функции
Lim((x^2-9)/(x-3), x=3).
Решение: Имеем неопределенность типа 0/0. В числителе применяем формулу сокращенного умножения
и вычисляем нужній предел
Метод раскрытия неопределенности умножением на сопряженноеМетод применяют к пределам в которіхнеопределенность порождают иррациональные функции. Числитель или знаменатель превращается в точке вычисления в ноль и неизвестно как найти границу.
Пример 7. Найти предел функции
Lim((sqrt(x+2)-sqrt(7x-10))/(3x-6), x=2).
Решение: Представим переменную в формулу предела
При подстановки получим неопределенность типа 0/0.
Согласно теории пределов схема обхода данной особенности заключается в умножении иррационального выражения на сопряженное. Чтобы выражение не изменилось знаменатель нужно разделить на такое же значение
По правилу разности квадратов упрощаем числитель и вычисляем предел функции
Упрощаем слагаемые, создающие особенность в пределе и выполняем подстановку
Упрощаем слагаемые которые вносят особенность и находим предел функции
Пример 9. Найти предел функции
Lim((x^2+x-6)/(sqrt(3x-2)-2), x=2).
Решение: Подставим двойку в формулу
Получим неопределенность 0/0.
Знаменатель нужно умножить на сопряженный выражение, а в числителе решить квадратное уравнение или разложить на множители, учитывая особенность. Поскольку известно, что 2 является корнем, то второй корень находим по теореме Виета
Таким образом числитель запишем в виде
и подставим в предел
Сведя разницу квадратов избавляемся особенности в числителе и знаменателе
Приведенным образом можно избавиться особенности во многих примерах, а применение надо замечать везде где заданная разница корней превращается в ноль при подстановке. Другие типы пределов касаются показательных функций, бесконечно малых функций, логарифмов, особых пределов и других методик. Но об этом Вы сможете прочитать в перечисленных ниже статьях о пределах.
Вычисления пределов в МейплДанный материал полезен прежде всего для студентов. Возможно в программе обучения, а некоторые для себя изучает математические программы для облегчения обучения и проверки решений. Это могут быть математические пакеты MathСad, Мathematica, Maple. Вычисления пределов в Мейпл достаточно просто организовать даже новичку. Все что нужно - правильно ввести функцию предел которой находим.
> restart;
Предел первой функции из тех которые рассматривали в Мейпл иметь следующую запись. Жмем конце "Enter" и получим конечное значение пределов
> limit((x^2+3*x)/(2*x+5),x=3);
> limit((x^2+2*x)/(4*x^2+3*x-4),x=infinity);
Третий пример примет следующий вид:
Мэйпл без проблем находит первый замечательный предел
> limit(sin(x)/x,x=0);
Тема 4.6.Вычисление пределов
Предел функции не зависит от того, определена она в предельной точке или нет. Но в практике вычисления пределов элементарных функций это обстоятельство имеет существенное значение.
1. Если функция является элементарной и если предельное значение аргумента принадлежит ее области определения, то вычисление предела функции сводится к простой подстановке предельного значения аргумента, т.к. предел элементарной функции f ( x ) при х стремящемся к а . которое входит в область определения, равен частному значению функции при х=а. т.е. lim f(x)=f(a ).
2. Если х стремится к бесконечности или аргумент стремится к числу, которое не принадлежит области определения функции, то в каждом таком случае нахождение предела функции требует специального исследования.
Ниже приведены простейшие пределы, основанные на свойствах пределов, которые можно использовать как формулы:
Более сложные случаи нахождения предела функции:
рассматриваются каждый в отдельности.
В этом разделе будут приведены основные способы раскрытия неопределенностей.
1. Случай, когда при х стремящемся к а функция f ( x ) представляет отношение двух бесконечно малых величин
а) Сначала нужно убедится, что предел функции нельзя найти непосредственной подстановкой и при указанном изменении аргумента она представляет отношение двух бесконечно малых величин. Делаются преобразования, чтобы сократить дробь на множитель, стремящийся к 0. Согласно определению предела функции аргумент х стремится к своему предельному значению, никогда с ним не совпадая.
Вообще если ищется предел функции при х стремящемся к а . то необходимо помнить, что х не принимает значения а. т.е. х не равен а.
б) Применяется теорема Безу. Если ищется предел дроби, числитель и знаменатель которой многочлены, обращающиеся в 0 в предельной точке х=а. то согласно вышеназванной теореме оба многочлена делятся без остатка на х-а.
в) Уничтожается иррациональность в числителе или в знаменателе путем умножения числителя или знаменателя на сопряженное к иррациональному выражение, затем после упрощения дробь сокращается.
г) Используется 1-й замечательный предел (4.1).
д) Используется теорема об эквивалентности бесконечно малых и следующие б.м.
2. Случай, когда при х стремящемся к а функция f ( x ) представляет отношение двух бесконечно больших величин
а) Деление числителя и знаменателя дроби на наивысшую степень неизвестного.
б) В общем случае можно использовать правило
3. Случай, когда при х стремящемся к а функция f ( x ) представляет произведение бесконечно малой величины на бесконечно большую
Дробь преобразовывается к виду, числитель и знаменатель которой одновременно стремятся к 0 или к бесконечности. т.е. случай 3 сводится к случаю 1 или случаю 2.
4. Случай, когда при х стремящемся к а функция f ( x ) представляет разность двух положительных бесконечно больших величин
Этот случай сводится к виду 1 или 2 одним из следующих способов:
а) приведение дробей к общему знаменателю;
б) преобразование функции к виду дроби;
в) избавление от иррациональности.
5. Случай, когда при х стремящемся к а функция f ( x ) представляет степень, основание которой стремится к 1, а показатель к бесконечности.
Функция преобразовывается таким образом, чтобы использовать 2-й замечательный предел (4.2).
Пример. Найти .
Так как х стремится к 3. то числитель дроби стремится к числу 3 2 +3 *3+4=22, а знаменатель- к числу 3+8=11. Следовательно,
Здесь числитель и знаменатель дроби при х стремящемся к 2 стремятся к 0 (неопределенность вида ), разложим числитель и знаменатель на множители, получим lim(x-2)(x+2)/(x-2)(x-5)
Уровень 2. Пример. Приведем пример применения понятия предела функции в экономических расчетах. Рассмотрим обыкновенную финансовую сделку: предоставление в долг суммы S 0 с условием, что через период времени T будет возвращена сумма ST . Определим величину r относительного роста формулой
Относительный рост можно выразить в процентах, умножив полученное значение r на 100.
Из формулы (1) легко определить величину ST .
При расчете по долгосрочным кредитам, охватывающим несколько полных лет, используют схему сложных процентов. Она состоит в том, что если за 1-й год сумма S 0 возрастает в (1 + r ) раз, то за второй год в (1 + r ) раз возрастает сумма S 1 = S 0 (1 + r ), то есть S 2 = S 0 (1 + r ) 2. Аналогично получается S 3 = S 0 (1 + r ) 3. Из приведенных примеров можно вывести общую формулу для вычисления роста суммы за n лет при расчете по схеме сложных процентов:
В финансовых расчетах применяются схемы, где начисление сложных процентов производится несколько раз в году. При этом оговариваются годовая ставка r и количество начислений за год k. Как правило, начисления производятся через равные промежутки времени, то есть длина каждого промежутка Tk составляет часть года. Тогда для срока в T лет (здесь T не обязательно является целым числом) сумма ST рассчитывается по формуле
где — целая часть числа. которая совпадает с самим числом, если, например, T. целое число.
Пусть годовая ставка равна r и производится n начислений в год через равные промежутки времени. Тогда за год сумма S 0 наращивается до величины, определяемой формулой
В теоретическом анализе и в практике финансовой деятельности часто встречается понятие “непрерывно начисляемый процент”. Чтобы перейти к непрерывно начисляемому проценту, нужно в формулах (2) и (3) неограниченно увеличивать соответственно, числа k и n (то есть устремить k и n к бесконечности) и вычислить, к какому пределу будут стремиться функции ST и S 1. Применим эту процедуру к формуле(3):
Заметим, что предел в фигурных скобках совпадает со вторым замечательным пределом. Отсюда следует, что при годовой ставке r при непрерывно начисляемом проценте сумма S 0 за 1 год наращивается до величины S 1 *. которая определяется из формулы
Пусть теперь сумма S 0 предоставляется в долг с начислением процента n раз в год через равные промежутки времени. Обозначим re годовую ставку, при которой в конце года сумма S 0 наращивается до величины S 1 * из формулы (4). В этом случае будем говорить, что re — это годовая ставка при начислении процента n раз в год, эквивалентная годовому проценту r при непрерывном начислении. Из формулы (3) получаем
Приравнивая правые части последней формулы и формулы (4), полагая в последней T = 1, можно вывести соотношения между величинами r и re .
Эти формулы широко используются в финансовых расчётах.
 (см. пример ).
(см. пример ).
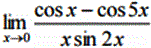 ,
, 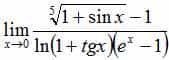
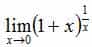 ,
, 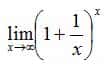 ,
, 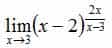
Вычислить указанные пределы:
3.  . Так как числитель и знаменатель обратились в нуль при x=4. то 4 – корень обоих многочленов, а значит, каждый из них разлагается на множители, одним из которых будет (x-4). Получаем
. Так как числитель и знаменатель обратились в нуль при x=4. то 4 – корень обоих многочленов, а значит, каждый из них разлагается на множители, одним из которых будет (x-4). Получаем
6.  – не существует, так как -1.
– не существует, так как -1.
7.  . Обозначим
. Обозначим  , причем заметим, что при x→16, y→2. Получим:
, причем заметим, что при x→16, y→2. Получим:
8.  . (Ответ получается непосредственно подстановкой (-∞) вместо x .)
. (Ответ получается непосредственно подстановкой (-∞) вместо x .)
9.  . Здесь следует рассмотреть односторонние пределы:
. Здесь следует рассмотреть односторонние пределы:
Следовательно,  – не существует (так как у функции разные односторонние пределы).
– не существует (так как у функции разные односторонние пределы).
Найти пределы функции, не применяя правило Лопиталя.
Ответ: 1/5
 Ответ: 1/6
Ответ: 1/6
Ответ: 1/e
Так как числитель и знаменатель обратились в нуль при x=1, то 1 – корень обоих многочленов, а значит, каждый из них разлагается на множители, одним из которых будет (x - 1).
В курсе математического анализа достаточно большой промежуток времени выделяется на изучение приемов того, как решать пределы, как для функций, так и для последовательностей. На данный момент существует некоторое количество уже готовых методов и правил, которые при правильном применении могут помочь решить довольно трудные задания с пределами.
В математический анализ были введены понятия того, как решать пределы функций, а также пределы последовательностей. Если необходимо вычислить предел последовательности, то запись этого примера выглядит так: lim xn=a. Из этой последовательности видно, что xn стремится к а. В свою очередь n наоборот стремится к бесконечности. Чаще всего последовательности представляются в виде рядов, таких как, например, р1, р2, р3. рm. рn. Все последовательности принято разделять на две группы: убывающие последовательности, а также возрастающие последовательности.
Как решать пределы: формулыЧаще всего величина, которая является переменной, например, х стремиться к конечному пределу, коим является величина а. При этом величина х постоянно приближается к величине а, в кто время как величина а остается постоянной. Запись этого сложного определения очень простая: limx =a. В этом случае n может стремиться к бесконечности, и к нулю. Существуют особые функции, которые называются бесконечными. В них предел также стремится к бесконечности. Если же рассматривается другая функция, которая описывает замедление хода чего-либо, то тут есть смысл говорить и о пределе, который будет стремиться к нулю.
Все приделы имеют свой определенный ряд свойств. Чаще всего у одной функции может быть лишь один предел. Это и есть наиболее важное и самое главное свойство пределов. Все остальные свойства пределов связаны с их определением и решением задач. Также студентам стоит обратить внимание на тему о том, как решать пределы с корнями.
Если в задании предоставлена функция 1/х, для которой х стремится к бесконечности, то предел этой функции будет равен нуля. Если же х будет стремиться к нулю, то соответственно и предел этой функции будет равен бесконечности.
Существуют специальные исключения их этих правил для тригонометрических функций. Функция синуса х всегда стремится к единице. Когда эта функция приближается к нулю, для нее становится справедливым данное тождество: lim sin x/x=1.
Существуют также и такого рода задачи, где в процессе вычисления пределов появляется некоторая ситуация, называемая неопределенностью. Неопределенность – это та ситуация, в которой вычисление предела невозможно. Единственный метод решения таких задач – это использование правил Лопиталя. Все неопределенности принято делить на две категории: неопределенность вида ноль делить на ноль, а также неопределенность вида бесконечность делить на бесконечность. Если рассматривать предел lim f(x)/l(x), когда f(x0)=l(x0)=0, то в этом случае наблюдается явное возникновение неопределенности вида ноль делить на ноль. Для того, чтобы правильно решить эту задачу, обе функции должны быть подвергнуты сначала дифференцированию, а затем вычислению предела результата. Если рассматривать неопределенность вида ноль делить на ноль, то предел функции будет равен: lim f(x)/l(x)=lim f'(x)/l'(x) (при x стремящемуся к нулю).
Существуют специальные сервисы, где можно решить предел онлайн любой сложности. Например, сайт "Вычислить предел онлайн " предлагает стандартный подсчет предела функций при помощи специального калькулятора. Если же необходимо подсчитать предел последовательности, то лучше обратиться к онлайн-калькулятору пределов на сайте "Решение пределов онлайн ".
Определение 1. Число $a$ называется пределом функции $f(x)$ в точке $x_0$ (или при $x\rightarrow x_0),$ если для каждого числа $\varepsilon>0$ существует такое число $\delta>0,$ что для всех $x$ удовлетворяющих условию $0<|x-x_0|<\delta,$ выполняется неравенство $|f(x)-a|<\varepsilon.$
Число $a$ - предел функции $f(x)$ в точке $x_0:\,\,\,
\lim\limits_
\varepsilon>0 \exists\delta>0, \forall x: 0<|x-x_0|<\delta
\Rightarrow |f(x)-a|<\varepsilon.$
Число $a$ - не является пределом функции $f(x)$ в точке $x_0:\,\,\, \lim\limits_
$\exists \varepsilon>0$ такое, что для $ \forall\delta>0 \exists
x: 0<|x-x_0|<\delta \Rightarrow |f(x)-a|\geq\varepsilon.$
1) Если $f(x)$ и $g(x)$ имеют пределы в точке $x_0,$ то функции $f(x)\pm g(x)$ и $f(x)g(x)$ также имеют пределы в точке $x_0,$ причем
$$\lim\limits_
$$\lim\limits_
2) Для любого числа $C,\,\,\, \lim\limits_
f(x))=C\lim\limits_
3) Если функции $f(x)$ и $g(x)$ имеют пределы в точке $x_0$ и $\lim\limits_
4) Пусть существует $\lim\limits_ a>g(y);$ тогда в точке $x_0$ существует предел композиции $g(f(x)),$ причем $\lim\limits_ x_0>g(f(x))=\lim\limits_ Если разность $f(x)-g(x)$ представляет собой неопределенность вида $\infty-\infty,$ или частное $\frac $$\lim\limits_
ПРЕДЕЛ ФУНКЦИЙ. Предел переменной величины. Бесконечно большая переменная величина
В этом параграфе мы будем рассматривать упорядоченные переменные величины, изменяющиеся специальным образом, который определяется терминами «переменная величина стремится к пределу». Во всем дальнейшем курсе понятие предела переменной будет играть фундаментальную роль, так как с ним непосредственно связаны основные понятия математического анализа -производная, интеграл и др.
Определение 1. Постоянное число а называется пределом переменной величины х, если для каждого наперед заданного произвольно малого положительного числа  можно указать такое значение переменной х. что все последующие значения переменной будут удовлетворять неравенству
можно указать такое значение переменной х. что все последующие значения переменной будут удовлетворять неравенству
Если число  есть предел переменной величины х. то говорят, что х стремится к пределу
есть предел переменной величины х. то говорят, что х стремится к пределу  . и пишут:
. и пишут:
В терминах геометрических определение предела может быть сформулировано следующим образом:
Постоянное число  есть предел переменной, если для любой наперед заданной как угодно малой окрестности с центром в точке
есть предел переменной, если для любой наперед заданной как угодно малой окрестности с центром в точке  и радиусом
и радиусом  найдется такое значение х. что все точки, соответствующие последующим значениям переменной, будут находиться в этой окрестности.
найдется такое значение х. что все точки, соответствующие последующим значениям переменной, будут находиться в этой окрестности.
Замечание 1. Постоянную величину с часто рассматривают как величину переменную, все значения которой одинаковы: х = с.
Очевидно, что предел постоянной будет равен самой постоянной, т.к. всегда выполняется неравенство  при любом
при любом  .
.
Замечание 2. Из определения предела следует, что переменная величина не может иметь двух пределов. Действительно, если  и
и  ,
, . то х должен удовлетворять сразу двум неравенствам:
. то х должен удовлетворять сразу двум неравенствам:
при произвольном малом  . а это невозможно, если
. а это невозможно, если 
Замечание 3. Не следует думать, что каждая переменная величина имеет предел. Пусть переменная величина х последовательно принимает следующие значения  (рис. 1).
(рис. 1).
При достаточно большом k значение  . и все последующие значения с четными номерами будут отличаться как угодно мало от единицы, а следующее значение
. и все последующие значения с четными номерами будут отличаться как угодно мало от единицы, а следующее значение  и все последующие значения х с нечетными номерами будут как угодно мало отличаться от нуля. Следовательно, переменная х не стремится к пределу.
и все последующие значения х с нечетными номерами будут как угодно мало отличаться от нуля. Следовательно, переменная х не стремится к пределу.
В определении предела указано, что если переменная величина стремится к пределу  . то
. то  - постоянное число. Но понятие «стремится» употребляется и для характеристики другого способа изменений переменной величины, что видно из следующего определения.
- постоянное число. Но понятие «стремится» употребляется и для характеристики другого способа изменений переменной величины, что видно из следующего определения.
Определение 2. Переменная х стремится к бесконечности, если для каждого наперед заданного положительного числа М можно указать такое значение х. начиная с которого все последующие значения переменного будут удовлетворять неравенству  .
.
Если переменная х стремится к бесконечности, то ее называют бесконечно большой переменной величиной и пишут  .
.
Предел функции
Рассмотрим некоторые случаи изменения функции при стремлении аргумента х к некоторому пределу а или к бесконечности.
Определение 1. Пусть функция  определена в некоторой окрестности точки а или в некоторых точках этой окрестности. Функция
определена в некоторой окрестности точки а или в некоторых точках этой окрестности. Функция  стремится к пределу
стремится к пределу  при х, стремящемся к
при х, стремящемся к  . если для каждого положительного числа
. если для каждого положительного числа  . как бы мало оно ни было, можно указать такое положительное число
. как бы мало оно ни было, можно указать такое положительное число  . что для всех х. отличных от
. что для всех х. отличных от  и удовлетворяющих неравенству
и удовлетворяющих неравенству  . имеет место неравенство
. имеет место неравенство
Если  есть предел функции f(x) при
есть предел функции f(x) при  . то пишут:
. то пишут: или f ( x )
или f ( x ) при
при  .
.
Если  при
при  . то на графике функции
. то на графике функции  . т.к. из неравенства
. т.к. из неравенства  следует неравенство
следует неравенство  . то это значит, что для всех точек х. отстоящих от точки
. то это значит, что для всех точек х. отстоящих от точки  не далее чем на
не далее чем на  . точки М графика функции
. точки М графика функции  лежат внутри полосы шириной
лежат внутри полосы шириной  . ограниченной прямыми
. ограниченной прямыми  и
и  (рис. 2).
(рис. 2).
Рассмотрим переменную величину у = f (х ). При этом считать, как и всюду в дальнейшем, что из двух значений функции последующим является то значение, которое соответствует последующему значению аргумента. Если определенная так переменная величина у при  стремится к некоторому пределу
стремится к некоторому пределу  . то будем писать
. то будем писать
и говорить, что функция у = f (х ) стремится к пределу b при  .
.
Легко доказать, что оба определения предела функции эквивалентны. Замечание.
Если f ( x ) стремится к пределу b 1 при х, стремящемся к некоторому числу  так, что x принимает только значения, меньшие
так, что x принимает только значения, меньшие  . то пишут
. то пишут  и называют b 1 пределом функции f ( x ) в точке
и называют b 1 пределом функции f ( x ) в точке  слева. Если х принимает только значения большие, чем
слева. Если х принимает только значения большие, чем  . то пишут
. то пишут  и называют b 2. пределом функции в точке
и называют b 2. пределом функции в точке  справа.
справа.
Можно доказать, что если, предел справа и предел слева существуют и равны, т. е.  . то b и будет пределом в смысле данного выше определения предела в точке
. то b и будет пределом в смысле данного выше определения предела в точке  . И обратно, еслт предел функции b в точке
. И обратно, еслт предел функции b в точке  . то существуют пределы функции в точке
. то существуют пределы функции в точке  справа и слева и они равны.
справа и слева и они равны.
Замечание.
Для существования предела функции при  не требуется, чтобы функция была определена в точке
не требуется, чтобы функция была определена в точке  . При нахождении предела рассматриваются значения функции в окрестности точки
. При нахождении предела рассматриваются значения функции в окрестности точки  . отличные от
. отличные от  ; это положение наглядно иллюстрируется следующим примером.
; это положение наглядно иллюстрируется следующим примером.
Пример. Докажем, что  . Здесь функция
. Здесь функция  не определена при х = 2.
не определена при х = 2.
Нужно доказать, что при произвольном  найдется такое
найдется такое  . что будет выполняться неравенство
. что будет выполняться неравенство
если | х — 2 | <  . Но при х
. Но при х  2 неравенство (1) эквивалентно неравенству
2 неравенство (1) эквивалентно неравенству
Таким образом, при произвольном  неравенство (1) будет выполняться, если будет выполняться неравенство (2) (здесь
неравенство (1) будет выполняться, если будет выполняться неравенство (2) (здесь  ). А это и значит, что данная функция при
). А это и значит, что данная функция при  имеет пределом число 4.
имеет пределом число 4.
Рассмотрим некоторые случаи изменения функции при  . Определение 2. Функция f ( x ) стремится к пределу
. Определение 2. Функция f ( x ) стремится к пределу  . если для каждого произвольно малого положительного числа
. если для каждого произвольно малого положительного числа  можно указать такое положительное число N. что для всех значении х. удовлетворяющих неравенству
можно указать такое положительное число N. что для всех значении х. удовлетворяющих неравенству  . будет выполняться неравенство
. будет выполняться неравенство  .
.
 Зная смысл символов:
Зная смысл символов:  очевидным является и смысл выражений:
очевидным является и смысл выражений:
 стремится к b при
стремится к b при  и
и
 стремится к b при
стремится к b при  .
.
которые символически записываются так:
Функция, стремящаяся к бесконечности,
Ограниченные функции
Итак, рассмотрены случаи, когда функция f ( x ) стремится к некоторому пределу b при  или при
или при  .
.
Рассмотрим тетерь случай, когда функция у = f (х) стремится к бесконечности при некотором способе изменения аргумента.
Определение 1. Функция f ( x ) стремится к бесконечности при  , т. е. является бесконечно большой величиной при
, т. е. является бесконечно большой величиной при  .
.
если для каждого положительного числа М. как бы велико оно ни было, можно найти такое  . что для всех значений х. отличных от а. удовлетворяющих условию
. что для всех значений х. отличных от а. удовлетворяющих условию  , имеет место неравенство
, имеет место неравенство  .
.
Если f ( x ) стремится к бесконечности при  . то пишут:
. то пишут:
или  при
при  .
.
Если f(x) стремится к бесконечности при  и при этом принимает только положительные или только отрицательные значения, соответственно пишут
и при этом принимает только положительные или только отрицательные значения, соответственно пишут  или
или  (рис. 4).
(рис. 4).
Бесконечно малые и их основные свойства
В параграфе будем рассматривать функции, стремящиеся к нулю при некотором характере изменения аргумента.
Определение. Функция  называется бесконечно малой при
называется бесконечно малой при  или при
или при  . если
. если  или
или  .
.
Теорема 1.
Если функция y = f(x) представляется в виде суммы постоянного числа b и бесконечно малой  .
.
y = b +  , (1)
, (1)
 (при
(при  ).
).
Обратно, если  . то можно написать
. то можно написать  . где
. где  — бесконечно малая.
— бесконечно малая.
Доказательство. Из равенства (1) следует. Но при произвольном  все значения
все значения  . начиная с некоторого, удовлетворяют соотношению
. начиная с некоторого, удовлетворяют соотношению  . следовательно, для всех значений у. начиная с некоторого, будет выполняться неравенство
. следовательно, для всех значений у. начиная с некоторого, будет выполняться неравенство  . А это и значит, что
. А это и значит, что  .
.
Обратно: если  . то при произвольном
. то при произвольном  для всех значений у. начиная с некоторого, будет
для всех значений у. начиная с некоторого, будет  . Но если обозначим
. Но если обозначим  . то, следовательно, для всех значений
. то, следовательно, для всех значений  . начиная с некоторого, будет
. начиная с некоторого, будет  . а это значит, что
. а это значит, что  — бесконечно малая.
— бесконечно малая.
Теорема 2.
Если  стремится к нулю при
стремится к нулю при  (или при
(или при  ) и не обращается в нуль, т o
) и не обращается в нуль, т o  стремится к бесконечности .
стремится к бесконечности .
Доказательство.
При любом, как угодно большом  будет выполняться неравенство
будет выполняться неравенство  . если только б y дет выполняться неравенство
. если только б y дет выполняться неравенство  . Последнее неравенство будет выполняться для всех значений
. Последнее неравенство будет выполняться для всех значений  . начиная с некоторого, так как
. начиная с некоторого, так как  .
.
Теорема 3.
Алгебраическая сумма двух, трех и вообще определенного числа бесконечно малых есть функция бесконечно малая .
Доказательство.
Проведем доказательство для двух слагаемых, так как для любого числа слагаемых оно проводится аналогично.
Пусть  . где
. где  . Докажем, что при произвольном как угодно малом
. Докажем, что при произвольном как угодно малом  найдется
найдется  такое, что при удовлетворении неравенства
такое, что при удовлетворении неравенства  будет выполняться неравенство
будет выполняться неравенство  . Так как
. Так как  есть бесконечно малая, то найдется такое
есть бесконечно малая, то найдется такое  что в окрестности с центром в точке a в радиусом
что в окрестности с центром в точке a в радиусом  будет
будет
Так как  есть бесконечно малая, то найдется такое
есть бесконечно малая, то найдется такое  . что в окрестности с центром в точке а и радиусом
. что в окрестности с центром в точке а и радиусом  будет
будет
Возьмем  равным меньшему из величин
равным меньшему из величин  и
и  . тогда в окрестности точки а с радиусом
. тогда в окрестности точки а с радиусом  будут выполняться неравенства
будут выполняться неравенства  ;
;  . Следовательно, в этой окрестности будет
. Следовательно, в этой окрестности будет
т. е.  . ч. т. д.
. ч. т. д.
Аналогично приводится доказательство и для случая, когда
Теорема 4.
Произведение функции бесконечно малой  на функцию ограниченную z = z (х) при
на функцию ограниченную z = z (х) при  (или
(или  ) есть величина (функция) бесконечно малая.
) есть величина (функция) бесконечно малая.
Доказательство.
Проведем доказательство для случая  . Для некоторого
. Для некоторого  найдется такая окрестность точки х = а. в которой будет удовлетворяться неравенство
найдется такая окрестность точки х = а. в которой будет удовлетворяться неравенство  . Для всякого
. Для всякого  найдется окрестность, в которой будет выполняться неравенство
найдется окрестность, в которой будет выполняться неравенство  . В наименьшей из этих двух окрестностей будет выполняться неравенство
. В наименьшей из этих двух окрестностей будет выполняться неравенство
А это и значит, что  —бесконечно малая. Для случая
—бесконечно малая. Для случая  доказательство проводится аналогично.
доказательство проводится аналогично.
Из данной теоремы вытекают:
Следствие 1. Если  , lim
, lim =
= 0, т o lim
0, т o lim =0, так как
=0, так как  есть величина ограниченная. Это справедливо для любого конечного числа множителей.
есть величина ограниченная. Это справедливо для любого конечного числа множителей.
Следствие 2. Если  и c = const. то lim ca = 0.
и c = const. то lim ca = 0.
Теорема 5.
Частное  от деления величины бесконечно малой
от деления величины бесконечно малой  (х) на функцию, предел которой отличен от нуля, есть величина бесконечно малая.
(х) на функцию, предел которой отличен от нуля, есть величина бесконечно малая.
Доказательство.
Пусть  На основании теоремы, что 1/
На основании теоремы, что 1/ есть величина ограниченная. Поэтому дробь
есть величина ограниченная. Поэтому дробь  есть произведение величины бесконечно малой на величину ограниченную, т. е. величина бесконечно малая.
есть произведение величины бесконечно малой на величину ограниченную, т. е. величина бесконечно малая.
Бесконечно малые функции  и
и  называются эквивалентными, если
называются эквивалентными, если  . Эквивалентность обозначается символом “
. Эквивалентность обозначается символом “
”, т.е. пишут 
Об эквивалентных бесконечно малых функциях известны следующие теоремы:
Т е о р е м а I. Предел отношения двух бесконечно малых функций не изменится, если эти бесконечно малые заменить им эквивалентным.
Т е о р е м а II. Для того чтобы две бесконечно малые функции были эквивалентными, необходимо и достаточно, чтобы их разность была бесконечно малой более высокого порядка по сравнению с каждой из них.
Если при некотором предельном переходе функция  есть функция бесконечно малая, то:
есть функция бесконечно малая, то:
Основные теоремы о пределах
Проведем доказательство для одного случая, так как для других доказательство проводится аналогично. Не будем писать ни  . ни
. ни  . подразумевая то или другое.
. подразумевая то или другое.
Теорема 1.
Предел алгебраической суммы двух, трех и вообще определенного числа переменных равен алгебраической сумме пределов этих переменных.
Доказательство.
Проведем доказательство для двух слагаемых, так как для любого числа слагаемых оно проводится так же. Пусть  .
.  . Тогда на основании теоремы можем написать:
. Тогда на основании теоремы можем написать:
где  и
и  —бесконечно малые. Следовательно,
—бесконечно малые. Следовательно,
Так как  есть постоянная величина, а
есть постоянная величина, а  - величина бесконечно малая, то снова по теореме заключаем, что
- величина бесконечно малая, то снова по теореме заключаем, что
Теорема 2.
Предел произведения двух, трех и вообще определенного числа переменных равен произведению пределов этих переменных
Доказательство.
Для сокращения записи приведем доказательство для двух множителей. Пусть  .
.  . Следовательно,
. Следовательно,
Произведение . есть величина постоянная. Величина
. есть величина постоянная. Величина  на основании теорем есть величина бесконечно малая. Следовательно,
на основании теорем есть величина бесконечно малая. Следовательно,  .
.
Следствие. Постоянный множитель можно выносить за знак предела.
Действительно, если  . с —постоянная и, следовательно,
. с —постоянная и, следовательно,  . то
. то  , ч. т. д.
, ч. т. д.
Теорема 3.
Предел частного двух переменных равен частному пределов этих переменных, если предел знаменателя отличен от нуля.
Доказательство.
Пусть  .
.  . Следовательно,
. Следовательно,  . где
. где  и
и  - бесконечно малые.
- бесконечно малые.
Напишем тождества
Дробь  есть постоянное число, а дробь
есть постоянное число, а дробь  по теоремам есть бесконечно малая переменная величина, так как
по теоремам есть бесконечно малая переменная величина, так как  есть бесконечно малая, а знаменатель
есть бесконечно малая, а знаменатель  имеет пределом
имеет пределом  .
.
Следовательно,  .
.
Доказать, исходя из определения предела, что  .
.
Р е ш е н и е. Пусть  -любое положительное число. Требуется доказать, что можно подобрать такое
-любое положительное число. Требуется доказать, что можно подобрать такое  , что для всех x. удовлетворяющих неравенству
, что для всех x. удовлетворяющих неравенству  . будет выполняться неравенство
. будет выполняться неравенство  .
.
Если  ,то
,то  и
и  .
.
Для выполнения неравенства достаточно потребовать, чтобы  т.е.
т.е.  откуда
откуда  (второй корень
(второй корень  отбрасывается, так как
отбрасывается, так как  ).
).
Таким образом, для любого  найдено такое
найдено такое  . что из неравенства
. что из неравенства  следует неравенство
следует неравенство  . т.е.
. т.е. 
Доказать, исходя из определения предела, что  .
.
Р е ш е н и е. Пусть  - любое положительное число. Требуется доказать, что можно подобрать такое
- любое положительное число. Требуется доказать, что можно подобрать такое  . что для всех x. удовлетворяющих неравенству
. что для всех x. удовлетворяющих неравенству  . будет выполняться неравенство
. будет выполняться неравенство 
Если  . то
. то  и
и
Следовательно, для выполнения неравенства  достаточно найти М из условия
достаточно найти М из условия  . т.е.
. т.е.  . Итак, для любого
. Итак, для любого  найдено такое М, что из неравенства
найдено такое М, что из неравенства  следует неравенство
следует неравенство  . т.е. доказано, что
. т.е. доказано, что  .
.
2. Основные теоремы о пределах функции. При вычислении пределов необходимы следующие теоремы
 , С - постоянная; (1)
, С - постоянная; (1)
 . С – постоянная; (2)
. С – постоянная; (2)
если  и
и  существуют, то
существуют, то
 . если
. если  (5)
(5)
Кроме того, мы будем пользоваться, тем что, для всех основных элементарных функций в любой точке их области определения имеет место равенство
Пример 3.
Р е ш е н и е. Из формул (2), (4), (1), (3) следует, что
Р е ш е н и е. Используем формулы (4), (3), (5):
Р е ш е н и е. так как  и
и  . то, используем формулу (6), получим
. то, используем формулу (6), получим
Замечание. Как показывают решения приведенных задач, в простейших случаях нахождения предела сводится к подстановке в данное выражение предельного значения аргумента. Часто, однако, приходится, прежде чем перейти к пределу, проводить преобразования данного выражения.
В последующих задачах показывается, какими приемами обычно пользуются при таких преобразованиях.